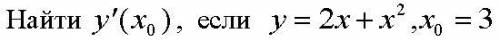

2. Квадрат.
Пошаговое объяснение:
Точки M и M1 симметричны относительно некоторой точки O , если точка O является серединой отрезка MM1. Тогда точка O называется центром симметрии.
Для 2-фигуры, то есть для квадрата точка пересечения диагоналей будет центром симметрии (см. рисунок).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
У квадрата четыре осей симметрии (см. рисунок).

2. Квадрат.
Пошаговое объяснение:
Точки M и M1 симметричны относительно некоторой точки O , если точка O является серединой отрезка MM1. Тогда точка O называется центром симметрии.
Для 2-фигуры, то есть для квадрата точка пересечения диагоналей будет центром симметрии (см. рисунок).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
У квадрата четыре осей симметрии (см. рисунок).

1) 8 2)12 км/ч
Пошаговое объяснение:
1)
Сначала находим производную:
у' = 2+2х
вычислим значение производной в точке х₀=3:
у' (х₀)= у' (3) = 2+2*3 = 8
2) Пусть скорость первого велосипедиста х км/ч, тогда скорость второго (х-3) км/ч. Первый велосипедист был в пути 3 часа и за это время путь 3х км, второй за 3 часа 3*(х-3) км. Т.к расстояние между пунктами 63 км, составляем уравнение:
3х+3(х-3)=63
6х=72
х=12
ответ: скорость первого велосипедиста 12 км/ч