На 40 конфет теперь больше у Кати
Пошаговое объяснение:
Исходя из условия составим краткую запись для облегчения решения:
у Кати — x+80 конфет
у Димы — x конфет.
¼(x+80) = ¼x+20 конфет Катя отдала Диме, у неё стало: x+80-(¼x+20) = ¾x+60 конфет (мы ещё не посчитали отданные Кате мальчиком конфеты).
Дима отдал Кате ¼x конфет, у него стало: x-¼x = ¾x конфет (мы ещё не посчитали отданные Диме девочкой конфеты).
В конечном итоге у Кати стало: ¾x+60+¼x = x+60 конфет.
В конечном итоге у Димы стало: ¾x+(¼x+20) = ¾x+¼x+20 = x+20 конфет.
Ответим на главный вопрос задачи: теперь у Кати на x+60-(x+20) = x+60-x-20 = 40 конфет больше.
ДАНО: Y(x) = 9/4*x⁴ - 13/3*x² + 1/2 .
ИССЛЕДОВАНИЕ:
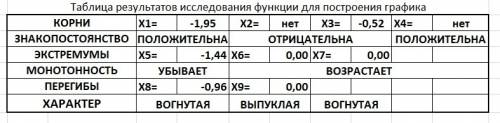
Заполняем таблицу - таблица в приложении.
Описание ГЛАЗАМИ: Функция четвертого порядка с положительным коэффициентом - примерно парабола и ветви вверх. Должно быть четыре корня.
1. Область определения. Непрерывная. Разрывов нет.
Dx = (-∞;+∞)
2. Корни функции: х1 = - 1,95 и х3 = -0,52. Двух других нет. Нахождение самих корней - без комментариев.
3. Интервалы знакопостоянства (дополнительно к таблице).
Положительна: Y>0 X∈(-∞;-1.95)∪(-0.52;+∞) - вне корней.
Отрицательна: Y<0 X∈(-1.95;-0.52) - между корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 9*x³ +13*x² = x²*(x + 13/9) = 0
Точки экстремумов: x 5 = - 13/9 (- 1,44), x6 = 0, x7 = 0
5 Ymin(х5) = Y(-1,44) = , Ymax(х6) = Y(x7) = (не максимальное) = +∞
6. Интервалы монотонности.
Убывает: Х∈(-∞;x5=-0.96) Возрастает: Х∈(х5=-0,96;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 27*x² +26х = х*(х + 26/27) = 0
x8 = - 26/27 (≈-0,96) и х9 = 0 - точки перегиба.
8. Вогнутая - "ложка" - Х∈(-∞;х8=-0,96)∪(х9=0;+∞) - вне корней.
Выпуклая - "горка" - Х∈(х8=-0,96);(х9=0))
Строим график - график на рисунке в приложении.