Итак, цена баранины за 1 кг - 250 р., цена телятины на 1 кг - 290 р. Пусть кол-во баранины = х кг, а кол-во телятины = у. Тогда, если баранины на 12 кг больше, чем телятины, то будет справедливо выражение:
х-12=у
Также нам известно, что масса баранины относится к массе телятины как 18:17, т.е.:
х = 18
у 17
Получаем систему уравнений:
х-12=у
х = 18
у 17
Из первого уравнения у подставим во второе:
х = 18
х-12 17
Решим его относительно х:
17х=18(х-12)
17х=18х-18*12
17х=18х-216
216=18х-17х
х=216 кг - масса проданной баранины.
Тогда масса проданной телятины будет:
х-12=у=216-12=204 кг
Нужно найти стоимость проданного мяса. Её мы найдём, как сумму денег, которую выручили за баранину и за телятину. Напомню, что, цена баранины за 1 кг - 250 р., цена телятины на 1 кг - 290 р. Масса проданной баранины 216 кг, масса проданной телятины 204 кг.
250*216+290*204=54000+59160=113160 р. - стоимость всего мяса.
sin x * (2 sin² x - 1) + cos² 2x = 0
cos 2x = 1 - 2 sin² x
-sin x * ( 1 - 2 sin² x ) + cos ² 2x = 0
- sin x * cos 2x + cos² 2x = 0 | : cos 2x (cos 2x ≠ 0)
cos 2x * ( - sin x + cos 2x) = 0
cos 2x * ( cos 2x - sin x ) = 0
cos 2x = 0
cos 2x - sin x = 0
1 - 2 sin² x - sin x = 0
- 2 sin² x - sin x + 1 = 0 | : (-1)
2 sin² x + sin x - 1 = 0
Пусть sin x = t, тогда
2t² + t - 1 = 0
D = 1² - 4 * 2 * (-1) = 1 + 8 = 9 = 3²
Вернёмся к замене:
sin x = 1/2
sin x = -1
ответ: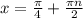
; 
; 
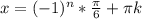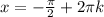, n∈Z ,k∈Z