1337) 12/24 16/24 18/24 4/24 9/24 10/24
1335) 4/5 3/5 6/7 2/3 5/8
1339) (6 1/4-4 1/8)*4+3 1/3:2 1/2 =9 5/6
1) 1/4-4 1/8=2 1/4-1/8=2 2/8-1/8=2 1/8
2) 1/8·4=17/8·4=17/2=8 1/2
3) 1/3:2 1/2= 10/3:5/2=10/3·2/5=4/3
4)8 1/2+1 1/3=9 3/6+ 2/6=9 5/6
(2 4/9+1 1/6)×1 4/5 -3 1/9÷ 2 1/3
1)2 4/9+1 1/6=2 8/18+1 3/18=3 11/18
2)3 11/18*1 4/5=13/2=6 1/2
3)3 1/9:2 1/3=28/9:7/3=4/3=1 1/3
4)6 1/2-1 1/3=6 3/6-1 2/6=5 1/6
(2-1 7/12)/(3 / 8 - 1 /6)* 3 1/4
1)2-1 7/12=1 12/12-1 7/12=5/12
2)3/8-1/6= 9-4/24=5/12
3)5/12:5/24=5/12*24/5=2
4)2/1*3 1/4=2/1*13/4=13/2=6 1/2
(7/10-2/5)*(1/4+5/6):6 1/2
1) 7/10-2/5=(7-4)/10=3/10
2) 1/4+5/6= (3+10)/12=13/12
3) 3/10*13/12:13/2=1/20
Пошаговое объяснение:
14.4 см
Пошаговое объяснение:
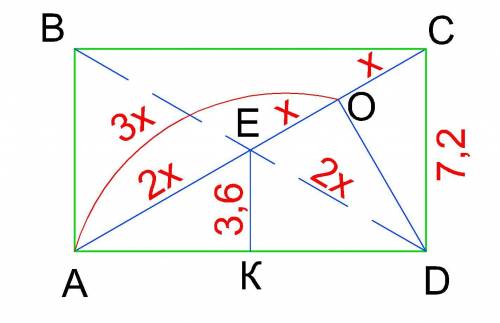
Побудуємо прямокутник ABCD, та проведемо в ньому діагоналі АС і BD, а також висоту DO до діагоналі АС і висоту EK із точки перетину діагоналей до більшої сторони AD.
Приймемо, що ОС=х,
тоді АС=4х.
Так як діагоналі прямокутника рівні і точкою перетину діляться навпіл, то АЕ=СЕ=ЕD=2х
і OE=CE-OC ⇒ OE=2x-x ⇒ OE=x.
Так як точка перетину діагоналей прямокутника є його геометричним центром, то CD=2EK=7.2 см.
Тоді, із прямокутного ΔCDO маємо:
OD²=CD²-OC² ⇒ OD²=51.84 - x²
Із прямокутного ΔEDO маємо:
OD²=ED²-OE² ⇒ OD²=4x² - x² ⇒ OD²=3x²
Отримуємо вираз:
51.84 - x² = 3x²
4x²=51.84
x=3.6
Тоді довжина діагоналі:
АС=4х=14.4 см
ответ: -20,4
Пошаговое объяснение:
сначала нужно раскрыть скобки: когда перед выражением в скобках стоит знак (+), тогда оно остаётся прежним.
7,6 - 23 -5 = -20,4