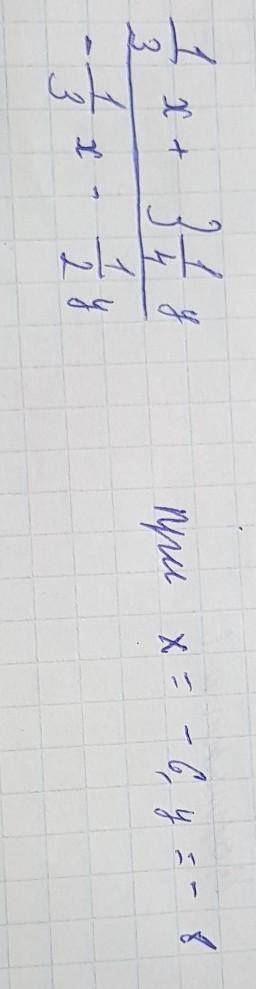
Имеем окружность с центром О(3,4) и радиусом 2.
Для начала убедимся, что прямая и окружность имеют общие точки. Для этого расчитаем расстояние от центра окружности до прямой:
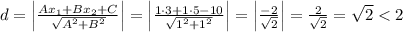
Расстояние от центра до прямой меньше радиуса, значит, окружность и прямая имеют две общие точки. Найдём их координаты. Для это запишем уравнение прямой в виде y=kx+b:
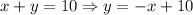
Подставим значение y в уравнение окружности и найдём абсциссы точек пересечения, решив получившееся квадратное уравнение:
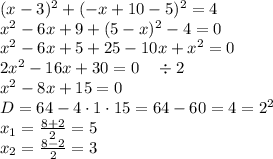
Тогда ординаты точек пересечения:
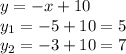
Таким образом, заданные окружность и прямая пересекаются в точках A(5,5) и B(3,7)
Для начала найдем, какая из точек является вершиной, а какие лежат в основании:
для этого найдем длину каждого из отрезков:
АВ= корень из ((-2-(-1))*(-2-(-1))+(-3-2)*(-3-2))= корень из (1+25)=корень из 26
АС= корень из ((-2-4)*(-2-4)+(-3-1)*(-3-1))= корень из (36+16)=корень из 52
ВС= корень из ((-1-4)*(-1-4)+(2-1)*(2-1))= корень из (25+1)=корень из 26
Значит АВ и ВС боковые стороны
осью симметрии данного треугольника будет являться высота, проведенная к основанию
найдем точку пересечения этой высоты с основанием: ((-2+4)/2;(-3+1)/2)=(1;-1) - H
вектор НА=(1+2;-1+3)=(3;2)
составим уравнение высоты:
х-1 у+1
--- =
3 2
воть
190/89
Пошаговое объяснение: