Находим вектор АС:
АС = (1-2; 8-1) = (-1; 7).
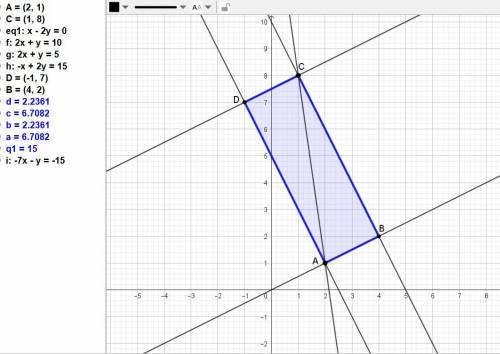
Уравнение АС: (x - 2)/(-1) = (y - 1)/7 каноническое, или 7х + у - 15 = 0 общее.
Стороны AD и BC перпендикулярны стороне АВ.
У перпендикулярной прямой коэффициенты А и В в уравнении меняются по сравнению с прямой АВ на (-В) и А (из условия, что их скалярное произведение равно 0).
Уравнение AD: 2x + у + С = 0. Подставим координаты точки А.
2*2 +1 + С = 0, отсюда С = -5.
Уравнение AD: 2x + у - 5 = 0.
Аналогично для стороны ВС.
Уравнение ВС: 2x + у + С = 0. Подставим координаты точки С.
2*1+ 8 + С = 0, отсюда С = -10.
Уравнение ВС: 2x + у - 10 = 0.
У параллельной стороны CD коэффициенты А и В сохраняются такие же, как и у АВ:
CD: х – 2у + C = 0. подставим координаты точки С.
1 - 2*8 + С = 0, отсюда С = 16 - 1 = 15.
Уравнение CD: x - 2y + 15 = 0.
Пошаговое объяснение:
60% = 60 : 100 = 0,6 = 6/10 = 3/5
Все книги = х штук
1 полка = 4/15х штук
2 полка = 3/5 * 4/15х = 12/75х = 4/25х штук
3 полка = 4/15х - 8 штук
4 полка = 2 * 4/25х = 8/25х штук
4/15х + 4/25х + 4/15х - 8 + 8/25х = х
20/75х + 12/75х + 20/75х - 8 + 24/75 = х
76/75х - 8 = х
1. 1/75х - х = 8
1/75х = 8
х = 8 : 1/75
х = 8 * 75/1
х = 600
Все книги = (х) = 600 штук
1 полка = (4/15х) = 4/15 * 600 = 4/1 * 40 = 160/1 = 160 книг
2 полка = (4/25х) = 4/25 * 600 = 4/1 * 24 = 96 книг
3 полка = (4/15х - 8) = 160 - 8 = 152 книги
4 полка = (8/25х) = 8/25 * 600 = 8/1 * 24 = 192 книги
160 + 96 + 152 + 192 = 600