Пошаговое объяснение:
Дано:
d = 16 см (диаметр окружности);
l AB l -10 см (длина секущей).
Найти:
Расстояние между прямыми а и в
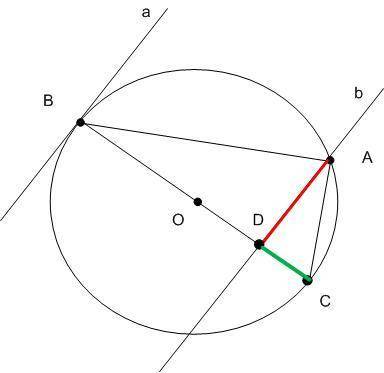
Выполним дополнительные построения (см. рис. "касательная и секущая".
l ВС l = d - диаметр, Δ ABC - прямоугольный, прямой угол ∠А (как треугольник, опирающийся на диаметр).
Найдем величину l AC l (по теореме Пифагора):
l AC l=√(d²- l AB l²);
l AC l=√(16²-10²)=√(256-100)=√156=2√39;
Т.к. прямые а и в параллельны, то ∠ ADB - прямой. И, следовательно,
расстояние между касательной а и секущей в - l BD l равно диаметру окружности минус отрезок l DС l.
l BD l = d - l DС l
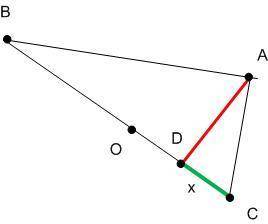
Обозначим длину отрезка l DС l через х.
Рассмотрим поближе Δ ABC и Δ ADC (см рис. "подобные треугольники"). Эти треугольники прямоугольные, и, что самое важное, эти треугольники подобные (они имеют равные острые углы. ∠ACD = ∠ACB)!
А, как известно, у подобных треугольников стороны пропорциональны. Составим пропорцию (вспомнив, что против равных углов лежат пропорциональные стороны):
l AC l/x=d/l AC l;
x=l AC l²/d;
x=(2√39)²/16=(4*39)/16=39/4;
l BD l = d - l DС l ⇒ l BD l = d - x;
l BD l =16-39/4=64/4-39/4=25/4=6 1/4=6.25
Пошаговое объяснение:
Пусть х кг овощей было в первом ящике, тогда
3х кг - во втором ящике,
5х кг - в третьем ящике.
Всего:
х + 3х + 5х = 9х
Может ли быть, что привезли 245 кг овощей? 216 кг? 127 кг?
Для того, чтобы ответить на этот вопрос, воспользуемся признаком делимости на 9.
Если сумма цифр числа делится на 9, то и число делится на 9
1) 2 + 4 + 5 = 11 - полученный результат не делится на 9, значит, овощей не могло быть 245 кг.
2) 2 + 1 + 6 = 9 - полученный результат делится на 9, значит, овощей могло быть 216 кг.
3) 1 + 2 + 7 = 10 - полученный результат не делится на 9, значит, овощей не могло быть 127 кг.
Найдём сколько килограмм в каждом ящике:
9х = 216
х = 216 : 9
х = 24 (кг) - в первом ящике.
24 · 3 = 72 (кг) - во втором ящике.
24 · 5 = 120 (кг) - в третьем ящике.
Проверка:
24 + 72 + 120 = 216
В цех привезли 216 кг овощей.
24 кг - в первом ящике;
72 кг - во втором ящике;
120 кг - в третьем ящике.