Question

РЕБЯТ , надо не просто упростить, а получить ответ в виде числа даю все, что есть

Answer 1

Упростить тригонометрическое выражение

$\displaystyle \frac{2(1-sin^{6}\alpha -cos^{6}\alpha ) }{1-sin^{4}\alpha -cos^{4}\alpha } =\\$  

1) Преобразуем числитель

1-sin⁶α-cos⁶α=1 - (sin⁶α+cos⁶α)=1 -( (sin²α)³+(cos²α)³)=cумма кубов=

=1 -(sin²α+cos²α) * (sin⁴α- sin²α*cos²α+cos⁴α)=

=1 -1 * (sin⁴α- sin²α*cos²α+cos⁴α)=

=1- (sin⁴α +2*sin²α*cos²α+cos⁴α- 3*sin²α*cos²α)=

=1-( (sin²α +cos²α)² - 3*sin²α*cos²α)=1-(1-3*sin²α*cos²α)=3*sin²α*cos²α.

2) Преобразуем знаменатель 1-sin⁴α-cos⁴α=1 - (sin⁴α+cos⁴α)=

=1 -( (sin²α)²+2sin²α *cos²α +(cos²α)²-2sin²α *cos²α ))=

=1 -( (sin²α+cos²α)² -2 sin²α*cos²α) = 1-(1-2 sin²α*cos²α)=2sin²α*cos²α/

$\displaystyle \frac{2*3sin^{2}\alpha *cos^{2} \alpha }{2*sin^{2}\alpha *cos^{2} \alpha } =3$

======================

Использован принцип добавления и вычитания слагаемых для получения формул сокращенного умножения;

sin²α+cos²α=1  основное тригонометрическое тождество ;

а³+в³=(а+в)(а² -ав+в²)  формула суммы кубов.

Answer 2

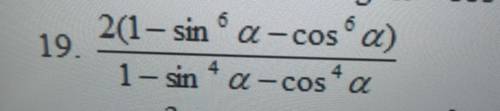
1)начнем плясать от основного тригонометрического тождества.

sin²α+cos²α=1

1²=1- верно?

поэтому 1=(sin²α+cos²α)²=sin⁴α+cos⁴α+2sin²α*cos²α; попутно для числителя

sin⁴α+cos⁴α=1-2sin²α*cos²α

Тогда знаменатель преобразуется с.о.

1-sin⁴α-cos⁴α=sin⁴α+cos⁴α+2sin²α*cos²α-sin⁴α-cos⁴α=2sin²α*cos²α.

2) Теперь числитель...по накатанной схеме. 1=1³

1-sin⁶α-cos⁶α=1³-(sin⁶α+cos⁶α)=

(sin²α+cos²α)³-(sin²α+cos²α)*(sin⁴α-cos²αsin²α+cos⁴α)=

(sin²α+cos²α)²-sin⁴α+cos²αsin²α-cos⁴α=

1²-(1-2sin²α*cos²α)+cos²αsin²α=1-1+2sin²α*cos²α+cos²αsin²α=3sin²α*cos²α;

3) делим числитель на знаменатель и умножаем на 2, получаем

2*3sin²α*cos²α/(2sin²α*cos²α)=3;

использовал формулу суммы кубов sin⁶α+cos⁶α=(sin²α)³+(cos²α)³=

(sin²α+cos²α)*(sin⁴α-cos²αsin²α+cos⁴α)

ОТВЕТ 3