
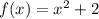 определена на множестве E
определена на множестве E 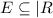
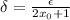 где
где 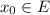 .
. на области
на области 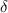 от
от  (то есть:
(то есть: 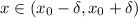 ) выполняется
) выполняется 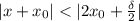 .
.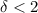 , выполняется
, выполняется 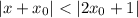 .
.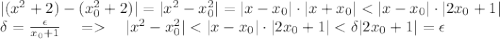
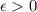 есть
есть 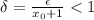 , на области которой выполняется
, на области которой выполняется 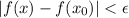
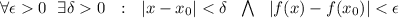 ). Следовательно -
). Следовательно - 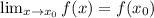 .
.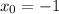 нужно отдельно доказать предел
нужно отдельно доказать предел 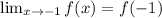 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 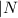 тоже подмножество
тоже подмножество  , значит
, значит 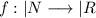 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 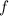 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 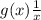 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 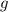 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 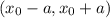 "...
"...
Для решения, нужно привести дроби к общему знаменателю.
Чтобы привести дроби к общему знаменателю, нужно найти их НОК (Наименьшее общее кратное), а затем каждую дробь домножить на коэфициент такой, чтобы дроби имели одинаковые знаменатели. Затем можно записать общий знаменатель, а все арифметические операции выполнить между числами числителей.
А)1/12+1/9+5/6= 3/12 + 4/36+ 30/36=37/36=1 целая 1/36
Б) 7/8-4/5+1/20=35/40-32/40+2/40=5/40= 1/8
В) 4/15+2/5+1/6=8/30+12/30+5/30=25/30=5/6
Г) 11/18-5/12-1/9=22/36-15/36-4/36=3/36=1/12