Не совсем понятно, могут ли повторяться цифры в числах компьютера.
Предположим, что цифры в числах повторяться могут. Если нами была выбрана хотя бы одна четная цифра, то всего четных чисел будет не меньше 
, так как на первых двух местах могут находиться любые цифры. Тогда, ответы на все вопросы задачи отрицательные.
Рассмотрим вариант, когда цифры в числах повторяться не могут.
Если нами была выбрана только одна четная цифра, то всего четных чисел мы можем составить 2 (четную цифру ставим на последнее место, двумя можно разместить оставшиеся цифры на первых двух местах).
Если нами были выбраны только две четные цифры, то двумя мы можем выбрать и поставить любую из них на последнее место, а еще двумя мы можем разместить оставшиеся две цифры на первых двух местах. Итого 
четных числа мы можем получить в этом случае.
Если нами были выбраны три четные цифры, то мы их можем переставлять любыми и в результате все равно получится четное число. Число перестановок для трех цифр дает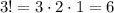 
четных чисел в этом случае.
Итак, мы можем получить ровно 2 чётных или ровно 4 чётных числа.
Из задания выходит, что задана правильная четырёхугольная пирамида SАВСД, высота SO которой равна ребру "a". Точка О - центр основания (точка пересечения его диагоналей).
Пусть длина ребра основания а = 1, диагональ основания d = √2.
Для определения угла между смежными боковыми гранями проведём сечение через диагональ ВД основания перпендикулярно боковому ребру . Получим равнобедренный треугольник ВКД, угол К которого равен углу между боковыми гранями.
Высоту из вершины К этого треугольника найдём как высоту h из вершины прямого угла в треугольнике SOД. Для этого найдём длину бокового ребра SД:
SД = √(1² + (√2/2)²) = √(1 + (2/4)) = √(3/2).
h = (1*(√2/2)/√(3/2) = 1/√3.
Теперь можно получить ответ:
угол ВКД = 2arc tg((d/2)/h) = 2arc tg((√2/2)/(1/√3)) = 2arc tg√(3/2) =
= 2*50,76848 = 101,537 градуса.