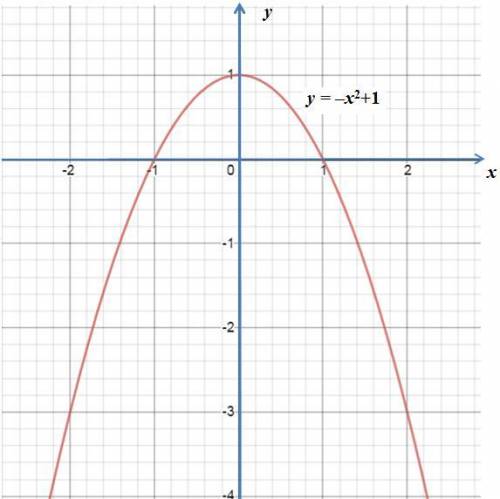
Дана функция: y = –x²+1 – парабола.
Определим абсциссу и ординату вершины параболы:
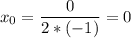
y₀ = y(x₀) = y(0) = –0²+1 = 1.
Определим нули функции:
y = 0 ⇔ –x²+1 = 0 ⇔ x² = 1 ⇔ x = ±1.
Так как перед x² коэффициент –1<0, то ветви параболы направлены вниз.
Чтобы определить, при каких значениях х функция принимает отрицательные значения, можно
использовать свойство параболы: так как y₀=1>0 и x₀=0∈[-1; 1], то на промежутке (-1; 1) функция принимает положительные значения, а в промежутках (–∞; –1) и ( 1; +∞) - отрицательные значения;
рассмотреть знак функции в промежутках (–∞; –1), (–1; 1), ( 1; +∞):
y = –x²+1 : – + –
------------------------(–1)--------------------(1)-----------------> x
Значит: в промежутках (–∞; –1) и ( 1; +∞) функция принимает отрицательные значения.
Для построения графика достаточно знать вершину и нули функции (график в приложении).
Все очень просто , для начала посмотрим на скобку(и то ,что в ней находится) , а так-же на степень.
1 шаг.
(c³)⁴ = c¹² , т.к. при возведение степени в степень , основание остается такое-же , а вот показатели степеней(в нашем случае ³ и ⁴ - перемножаются между собой.
2 шаг.
При c=3 , у нас получается выражение 3-⁸ (3 в минус восьмой степени) * 3¹² (3‐⁸ * 3¹²)
3 шаг.
3-⁸ * 3¹² = 3⁴ , т.к при умножение степеней с одинаковыми основаниями , основание остается без изменений , а показатели степеней складываются.
И того , если расписать получится -
c-⁸* (c³)⁴ = c-⁸ * c¹² = c⁴ = 3⁴ = 81