Это показательное уравнение вида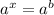 
, где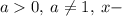 
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения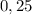 
представить в виде числа со степенью так, чтобы в основании было число 
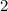. Это явно число 
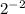(проверка: 
).
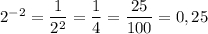Значит теперь, когда наше показательное уравнение имеет вид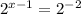 
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение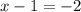 
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 
.
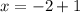Из этого следует, что ответ нашего показательного уравнения равен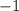 
.
если решением уравнения 2х = 10 является единственное число 5, то у уравнения cosx = 0 решений бесконечное множество, так как косинус обращается в ноль при:
π/2 + πk, где k∈Z (множеству целых чисел)
В данном случае k - переменная. Иногда вместо нее употребляется n. Принципиального различия в обозначении переменной нет.
Выглядит это так:
π/2 + πn, n∈Z.
Некоторые тригонометрические уравнения имеют решения с периодом 2π:
sinx = -1 ⇔ x = -π/2 + 2πn, n∈Z
При решении некоторых тригонометрических уравнений могут образоваться 2 разных корня. Например решением уравнения:
sin²x - sinx*cosx -2cos²x = 0
будут:
-π/4 + πk; arctg2 + πn, n;k ∈ Z
В этом случае n и k являются независимыми друг от друга переменными, поэтому для периода каждого корня используется разное ее обозначение.