1. 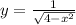
D(y): 4-x²>0 ⇔ (2-x)·(2+x)>0
Определим знак (2-x)·(2+x):
+ · - = - + · + = + - · + = -
-∞ --------[-100]-------(-2)------[0]------(2)-----[100]------> +∞
D(y)=(-2; 2)
2. 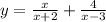
D(y): x+2≠0 и x-3≠0 ⇔ x≠-2 и x≠3
D(y)=(-∞; -2) ∪ (-2; 3) ∪ (3; +∞)
3. 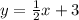
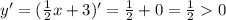
Значит, функция монотонно возрастает и поэтому точек экстремума нет.
4. y= -x²+4
y'= (-x²+4)'= (-x²)'+(4)'= -2·x+0= -2·x
y'(x)= 0 ⇔ -2·x=0 ⇒ x = 0
Для x < 0
y'(x)= -2·x >0, то есть для x∈(-∞; 0) функция монотонно возрастает,
а для x > 0
y'(x)= -2·x <0, то есть для x∈(0; +∞) функция монотонно убывает.
Тогда x = 0 является точкой максимума, то есть точкой экстремума.
Р = 2(150+180) = 2•330 = 660 см.
2) Площадь всех стен:
Sвсех ст. = 660•200 = 132000 кв.см.
3) Площадь двери:
Sдв. = 80•180 = 14400 кв.см.
4) Площадь стен за вычетом площади двери:
Sст. = S всех ст. - S дв. =
= 132000 - 14400 = 117600 кв.см.
5) Площадь пола:
Sпол. = 150•180 = 27000 кв.см.
6) Вся площадь, которая будет покрыта кафелем:
S = Sст + Sпол. = 117600 + 27000 =
= 144600 кв.см
7) Площадь одной кафельной плитки:
Sпл. = 15 • 25 = 375 кв.см,
8) Количество плиток, необходимое для проведения ремонта:
S : Sпл. = 144600 : 375 =
= 385,6 ≈ 386 плиток.
Мы округлили результат до 386, поскольку плитку при продаже не режут на части.
ответ: 386 плиток.