 - числитель исходной дроби, тогда
- числитель исходной дроби, тогда 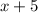 - знаменатель этой же дроби.
- знаменатель этой же дроби. 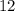 получилась дробь, которая в
получилась дробь, которая в 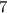 раз больше исходной. Так как знаменатель остался прежним, то числитель второй дроби в
раз больше исходной. Так как знаменатель остался прежним, то числитель второй дроби в 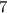 раз больше числителя исходной дроби.
раз больше числителя исходной дроби.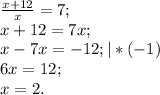
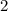 - числитель исходной дроби.
- числитель исходной дроби.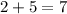 .
.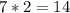 .
.
x меньше -2/11
Пошаговое объяснение:
просто просто решаешь уравнение