x > 2
Пошаговое объяснение:
Данное неравенство равносильно следующей системе:
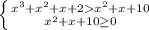
Первое неравенство системы - исходное, возведенное во вторую степень
Второе неравенство - ограничение на существование(т.к левая часть больше правой, которая неотрицательная, то условие на существование левой части можно не учитывать).
Запишем второе неравенство в виде уравнения и убедимся, что корней нет . Т.к. (D < 0), значит, парабола лежит выше оси Oy,следовательно, нет никаких ограничений на x.
В первом неравенстве системы получаем :
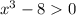 - разность кубов, которая раскладывается следующим образом:
- разность кубов, которая раскладывается следующим образом:
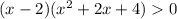
Второй множитель больше 0 при всех x из множества R, значит, достаточно, чтобы только x-2 > 0, то есть, x > 2
у пути / час - скорость 2
(х+у) - скорость сближения
(х+у) * 3 = 1 - весь путь
3 х - путь 1 пешехода до встречи
3у - путь 2 пеш до встречи
После встречи каждый пешеход шёл с прежней скоростью, но путь встречного путника.
(х+у ) * 3=1 }
3 х / у - 3у / х = 2,5}
х+у=1/3 }
3х² - 3у² = 2 1/2 ху}
х = 1/3 - у, подставим значение х во второе уравнение:
3 (1/3 - у)² - 3у² = 2 1/2у (1/3 - у)
3 (1/9 - 2/3у+у²) - 3у² = 5/6 у - 2 1/2 у²
1/3 - 2у +3у² - 3у² - 5/6у+2 1/2у² = 0
2 1/2 у² - 2 5/6 у +1/3 = 0
D = (17/6)² -1/3*4*2 1/2 = 289 /36 - 20/6 = 169/36
у = (17/6 - 13/6) :5 = 2/15 пути/ час скорость второго путника
х = 1/3 - 2/15 = 1/5 пути в час скорость первого путника
3х / у+3 = 3 * 1/5:2/15 +3 = 7 1/2 (час) - время в пути 2 путника
3 у /х+3=3* 2/15 : 1/5+3=5 (час) - время в пути 1 путника.