20
Пошаговое объяснение:
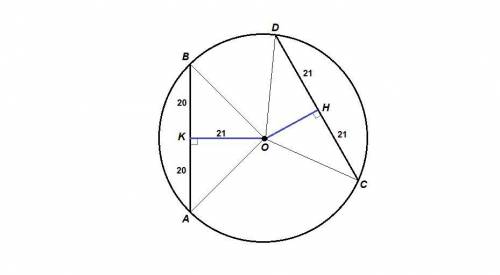
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и и OH⊥CD,
ОК = 21 - расстояние от центра до АВ,
ОН - искомое расстояние от центра до CD.
ΔОАВ равнобедренный, значит ОК - высота и медиана. ⇒
АК = КВ = 1/2АВ = 1/2 · 40 = 20
Из прямоугольного треугольника АКО по теореме Пифагора:
АО = √(АК² + КО²) = √(20² + 21²) = √(400 + 441) = √841 = 29
СО = АО = 29
ΔCOD равнобедренный, значит OН - высота и медиана, ⇒
СН = HD = 1/2CD = 1/2 · 42 = 21
Из прямоугольного треугольника СОН по теореме Пифагора:
OH = √(CO² - CH²) = √(29² - 21²) = √(841 - 441) = √400 = 20
4*4^x - (2*3)^x = 2*(3^2)*3^(2x)
4*(2²)^x - (2^x)*3^x =2*9*3^(2x)
4*2^(2x) -(2^x)*3^x =18*3^(2x)
Разделим обе части уравнения на (2^x)*3^x
4*(2^x)/(3^x) - 1 =18*(3^x)/(2^x)
4*((2/3)^x) - 1 =18*(3/2)^x
Сделаем замену переменных
(2/3)^x = у где у > 0
4y -1 = 18/y
Умножим обе части уравнения на у
4у² -у = 18
4у² -у - 18 = 0
D =1-4*4(-18) =1+288 =289
y1=(1-17)/8 =-16/8 =-2 не подходит так как y>0
y2=(1+17)/8 =18/8 = 9/4
Находим значение х при у = 9/4
(2/3)^x = 9/4
(2/3)^x = (3/2)²
x = -2
ответ:-2