1) 1 1/36 2) 5 5/16 3)1 13/28 4)6 34/50 5)5 43/84 6)2 7/90
Пошаговое объяснение:
11/18 + 5/12 (Наименьший общий знаменатель = 36, значит первую дробь умножаем на 2, вторую на 3) = 37/36 = 1 1/36
2 1/8+3 3/16 (отделяем целую и дробную часть, складываем) = 5 1/8+3/16 (наименьший общий знаменатель - 16, умножаем первую дробь на 2)= 5 2/16+3/16=5 5/16
3/4+5/7 (наименьший общий знаменатель = 28. Первую дробь умножаем на 7, вторую на 4)= 21/28+20/28=41/28=1 13/28
4 7/25+2 4/10( отделяем целую и дробную часть, складываем)= 6 7/25+4/10 (общий знаменатель =50. первую дробь на 2, вторую на 5)
=6 14/50+20/50=6 34/50
5/12+5 2/21(наименьший общий знаменатель =84. Первую дробь на 7, вторую складываем с целой частью и на 4 ) =463/84=5 43/84
1 11/18+7/15(наименьший общий знаменатель=90. Первую дробь складываем с целой частью и умножаем на 5, вторую на 6 и складываем) = 187/90=2 7/90
Используя теорему о высоте прямоугольного треугольника, и подобных треугольниках (см. картинку) - полетели:
61) Т.к. Δ BKC ≡ Δ CKA ⇒ Их стороны пропорционально равны, а это значит что:

63) Т.к. Δ BKC ≡ Δ CKA ⇒ Их стороны пропорционально равны, а это значит что:
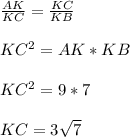
Далее рассмотрим Δ AKC:
В нём один катет AK = 9. Второй катет KC = 3√7. Остаётся найти гипотенузу AC. Применяем теорему Пифагора:
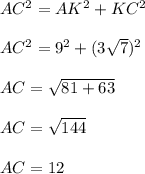
65) Т.к. AO и OB - это радиусы окружности ⇒

Далее:
AM = AO + OM = 10 + 6 = 16
⇒ MB = OB - OM = 10 - 6 = 4
Т.к. Δ ACM ≡ Δ CBM ⇒ Их стороны пропорционально равны, а это значит что:
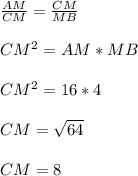
67) Т.к. Δ ACH ≡ Δ CBH ⇒ Их стороны пропорционально равны, а это значит что:

Далее: Рассмотрим Δ ACB
Применяем формулу площади прямоугольного треугольника через высоту, проведённую к его основанию:
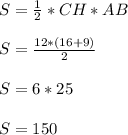

1/4*х+1/5*х=18
5х/20+4х/20=18
9х/20=18
9х=18*20
9х=360
х=360/9
х=40
проверка
1/4*40+1/5*40=10+8=18