Если m=1, то m является полным квадратом (), поэтому этот случай можно не рассматривать.
Пусть m>1 не является полным квадратом, тогда в разложении m на простые множители (существование такого разложения гарантируется основной теоремой арифметики)
хотя бы один показатель является нечетным числом. Не теряя общности, можно предположить, что это
По условию где a - целое число. Разделим это равенство на m:
Поскольку m+1 и na - целые числа, является целым числом, то есть делится на m, откуда делится на Отсюда следует, что n делится на следовательно делится на
Теперь мы уже на финише. Из последнего рассуждения следует, что делится на na, естественно, делится на но (m+1) ну никак не может делиться на поскольку соседние натуральные числа взаимно просты (а m делится на ).
Полученное противоречие доказывает, что m обязано быть полным квадратом.
РЕШЕНИЕ Уравнение касательной по формуле Y = k*x + b = y'(Xo)*(x -Xo)+ y(Xo) Уравнение производной y'(x) 2*1.5*x = 3*x = k. Вычисляем в точке касания. y'(2) = 6, y(2) = 1.5*4 = 6. Уравнение касательной Y = 6*(x - 2) + 6 = 6*x - 3 Находим пределы интегрирования - решаем уравнение: 1,5*x² + 3 = 6*x - 3 1.5*x² - 6*x + 6 = 0 a = x1=x2 = 2 b = 0 - дано Площадь - интеграл разности функций = 1.5*x²+3 -(6*x - 3) Вычисляем при а - S(2) = 4 Вычисляем при b - S(0) = 0 S = 4 - площадь - ОТВЕТ рисунок к задаче в приложении.
Делим все монеты на две равные кучки по 1007 монет и проводим их взвешивание. каждая кучка покажет разный вес.1010≠1010 (для примера левая легче)теперь из каждой из двух кучек откладываем по одной монете и делим их опять на две равные части по 505 монеты. получаем 4 кучки и 2 монетки.проводим попарное взвешивание.505=505 505=505 1 монетка≠1 монеткав этом случае берем из любой кучки монетку и взвешиваем с любой из двух монеток.505≠505 505=505 1=1значит фальшивая монетка легче505=505 505≠505 1=1значит фальшивая монетка тяжелее
Если m=1, то m является полным квадратом (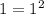 ), поэтому этот случай можно не рассматривать.
), поэтому этот случай можно не рассматривать.
Пусть m>1 не является полным квадратом, тогда в разложении m на простые множители (существование такого разложения гарантируется основной теоремой арифметики)
хотя бы один показатель является нечетным числом. Не теряя общности, можно предположить, что это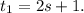
По условию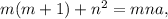 где a - целое число. Разделим это равенство на m:
где a - целое число. Разделим это равенство на m:
Поскольку m+1 и na - целые числа,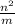 является целым числом, то есть
является целым числом, то есть 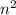 делится на m, откуда
делится на m, откуда 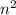 делится на
делится на 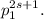 Отсюда следует, что n делится на
Отсюда следует, что n делится на 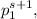 следовательно
следовательно 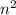 делится на
делится на 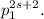
Теперь мы уже на финише. Из последнего рассуждения следует, что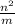 делится на
делится на 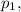 na, естественно, делится на
na, естественно, делится на 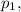 но (m+1) ну никак не может делиться на
но (m+1) ну никак не может делиться на 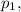 поскольку соседние натуральные числа взаимно просты (а m делится на
поскольку соседние натуральные числа взаимно просты (а m делится на 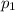 ).
).
Полученное противоречие доказывает, что m обязано быть полным квадратом.