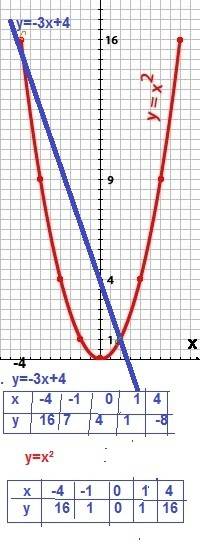
x ² =-3х+4 имеет два решения: x ₁ =1 и x ₂ =-4 .
. y=-3x+4 у=х²
х|-4|-1|0|1|4 x|-4|-1|0|1|4|
у|16|7|4|1|-8 y|16|1|0|1|16
построим графики полученных функций см приложение
Точки пересечения прямой y = -3x+4 c параболой y = x ²
имеют координаты (1; 1) и (-4; 16)
Абсциссы этих точек и являются
решением нашего уравнения
x 1 =1 , x 2 =-4 .
Проверка x ²=–3x+4 подставим наши значения вместо х
1²=-3*1+4 верно
-4²=-3*(-4)+4 верно
1) Площадь основания (ромба) So = a²sin 60° = 36*√3/2 = 18√3 см².
Проекция высоты боковой грани на основание - это половина высоты h основания: (h/2) = asin 60°/2 = 6*√3/(2*2) = 3√3/2 см.
Так как угол наклона боковой грани к основанию равен 45 градусов, то высота H пирамиды равна (h/2).
Отсюда находим объём пирамиды:
V = (1/3)SoH = (1/3)*(18√3)*(3√3/2) = 27 см³.
2) Проекция бокового ребра на основание равна стороне основания.
Площадь основания равна: So = a²3√3/2 = 1*3√3/2 = 3√3/2.
Объём пирамиды V = (1/3)SoH. Отсюда находим высоту пирамиды: Н = 3V/So = 3*6/(3√3/2) = 4√3.
Тогда боковое ребро L = 4√3*√2 = 4√6.