Пошаговое объяснение:
1.
(-0,5)⁻² - (2 1/4)⁻¹ ¹⁾² + (17/20)⁰ = 1/(0,5)² - (9/4)⁻³⁾² + 1 =
= 1/0,25 - (4/9)³⁾² + 1 = 100/25 - (2/3)³ + 1 =
= 4 - 8/27 + 1 = 5 - 8/27 = 4 19/27 (ответ 2),
2.
(к⁷⁾⁵ * м⁴⁾³) / (к³⁾¹⁰ * м⁷⁾³⁰) =
= к⁷⁾⁵⁻³⁾¹⁰ * м⁴⁾³⁻⁷⁾³⁰ = к¹⁴⁾¹⁰⁻³⁾¹⁰ * м⁴⁰⁾³⁰⁻⁷⁾³⁰ = к¹¹⁾¹⁰ * м³³⁾³⁰ =
= к¹¹⁾¹⁰ * м¹¹⁾¹⁰ = (км)¹¹⁾¹⁰ (ответ 4),
3.
((с⁻¹⁾⁷ * у⁻⁰°⁴)³ * с³⁾⁷ * у⁰°²)⁻¹ =
= (с⁻³⁾⁷ * у⁻¹°² * с³⁾⁷ * у⁰°²)⁻¹ =
= (с⁻³⁾⁷⁺³⁾⁷ * у⁻¹°²⁺⁰°²)⁻¹ = (с⁰ * у⁻¹)⁻¹ = (1 * у⁻¹)⁻¹ = (у⁻¹)⁻¹ =
= у⁻¹*⁽⁻¹⁾ = у¹ = у (ответ 3),
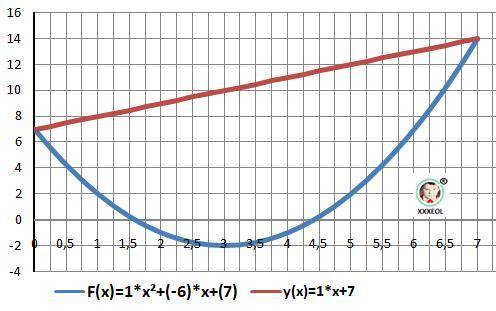
Дано: F(x) = x² -6*x + 7, y(x) = x+7
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков: F(x)=y(x).
- x²+7*x = х*(7 - х)=0 - квадратное уравнение
b = 0- верхний предел, a = 7- нижний предел.
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) =-7*x + *x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = -7/2*x² + 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(7) = 0 - 171 1/2 + 114 1/3 = -57 1/6
S(b) = S(0) =0+0+0 = 0
S = S(7)- S(0) = 57 1/6 - площадь - ответ (≈ 57.17)
Рисунок к задаче в приложении.