Изготовление стандартной детали и изготовление нестандартной детали - это противоположные события. Так как известны вероятности изготовления стандартной детали, то найдем вероятности изготовления нестандартной детали:
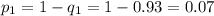
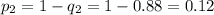
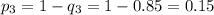
Теперь найдем вероятности того, что случайно выбранная деталь изготовлена в каждом из цехов. Такие вероятности можно определить как отношение соответствующего числа линий в этом цехе к общему числу линий на производстве:
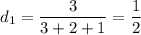
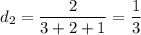
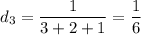
Тогда, искомая вероятность того, что наудачу взятая деталь на сборке окажется нестандартной, равна сумме попарных произведений вероятностей того, что деталь, изготовленная в определенном цехе, является нестандартной, на вероятности того, что деталь изготовлена в этом цехе:
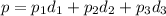
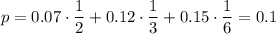
ответ: 0.1
Пошаговое объяснение:
В данных задачах присутствует много разных тем. Если с математикой уж совсем плохо, то что бы научиться решать допустим 1 уравнение, то придется выучить простейшие виды неравенств, их свойства и методы решений. В 1 неравенстве также присутствует логарифм, поэтому стоить выучить и его. 2 пример - это уровень 7 класса(достаточно знать действия с одночленами и многочленами). В 3 примере присутствует обратные тригонометрические функции, поэтому что ты уметь решать такие задачи стоить разобраться в разделе "тригонометрия")))
Пошаговое объяснение:
по формуле Виета
х1+х2 = -3/2 ⇒ -3+х2 = -3/2 ⇒х2 = 3-3/2 = 1,5
х1*х2 = а/2 ⇒-3*х2= а/2 ⇒ х2 = -а/6
приравняем правые части
-а/6 = 1,5
а = -1,5*6
а= -9