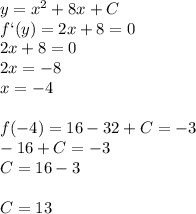
x^2 + mx + n = 0 имеет корень, который является целым числом.
Причем числа m и n простые.
m, n > 0
значит корни x1 x2 будут меньше 0, если существуют
(x + x1)(x + x2) = 0
x^2 + (x1 + x2)x + x1x2 = 0
x1*x2 = n
по начальным условиям корень x1 целый, а n - простое
то один из корней = -1 (корень x1)
Тогда применяем обратную теорему Виета
x1 + x2 = -m -1 + x2 = -m
x1*x2 = n x2 = - n
-1 - n = - m
m - n = 1 по условию m n - простые ,
единственная пара чисел, когда разница простых = 1 это 3 и 2
m = 3 n = 2
Найдите, чему равно m^2+n^2 .
3^2 + 2^2 = 9 + 4 = 13
нехорошо олимпиады размещать
1. Запиши данное число в виде десятичной дроби:
12 13/1000 =
1,213
2. Запиши в виде десятичной дроби:
4/125 =
0,032
3. Преобразуй 66 мин. в часы.
Представь в виде десятичной дроби:
1ч6мин=1,1ч
4. Запиши обыкновенную дробь в виде десятичной:
46/1000=
0,046
5. Запиши смешанное число в виде десятичной дроби.
15 5/10 =
155/10=15,5
6. Запиши десятичную дробь в виде смешанного числа.
В результате дробь сократи:
8,26=
8 26/100=8 13/50
в результате должна быть дробь с целым числом!
7. Найди, какая часть фигуры закрашена в жёлтый цвет.
(запиши в виде десятичной дроби).
8. Переведите обыкновенную дробь 23/180 в периодическую.
0,12(7)
9. Переведите периодическую дробь 0,2(6) в обыкновенную.
Для записи дроби используйте знак /.
0,2(6)=(26-2)/90=24/90=4/15