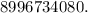НОД (2970, 5460) = 30
Разложим числа на простые множители и подчеркнем общие множители чисел:
2970 = 2 · 3 · 3 · 3 · 5 · 11
5460 = 2 · 2 · 3 · 5 · 7 · 13
Общие множители чисел: 2; 3; 5
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (2970; 5460) = 2 · 3 · 5 = 30
НОК (2100, 1350) = 18900
Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.
2100 = 2 · 2 · 3 · 5 · 5 · 7
1350 = 2 · 3 · 3 · 3 · 5 · 5
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (2100; 1350) = 2 · 2 · 3 · 5 · 5 · 7 · 3 · 3 = 18900
Всего десятизначных чисел составить можно 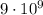 на первое место используется 9 цифр, так как 0 нельзя ставить, а на оставшиеся 9 мест - по 10 цифр). Теперь посчитаем сколько таких десятизначных чисел можно составить, если цифры не повторяются.
на первое место используется 9 цифр, так как 0 нельзя ставить, а на оставшиеся 9 мест - по 10 цифр). Теперь посчитаем сколько таких десятизначных чисел можно составить, если цифры не повторяются.
На первое место можно использовать 9 цифр, поскольку 0 не учитываем, на второе место - 9 цифр, т.к. одна цифра уже используется и цифра 0 учитывается, на третьем место — оставшиеся 8 цифра, ... и на десятом месте 1 цифра. Составить их можно
Итого 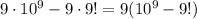 можно составить десятизначные числа, которые имеют хотя две одинаковые цифры
можно составить десятизначные числа, которые имеют хотя две одинаковые цифры
ответ: 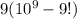 или
или