Язык ,9 класс ergänze die sätze mit passenden präpositionen und artikeln. 1) was hast du am samstag vor? - ich gehe konzert. 2) wo warst du gestern? - wir waren zirkus. 3) gehst du museum oft? - nein, nicht sehr oft. 4) möchtest du am sonntag disko gehen? - nein, ich fahre mit den eltern zu meiner oma. 5) ist tanja da? - nein, sie ist mit dem hund park gegangen. 6) ich möchte galerie gehen. kommst du mit? 7) ich habe hunger. gehen wir mal café! 8) wart ihr kino? - ja, wir haben einen neuen film gesehen.
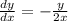
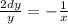 - уравнение с разделёнными переменными
- уравнение с разделёнными переменными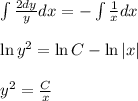
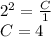
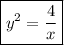 - частный интеграл.
- частный интеграл.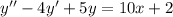
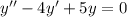
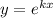 , тогда получаем
, тогда получаем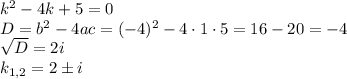
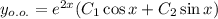
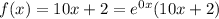
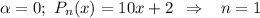
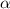 с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде:
с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде: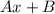
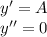
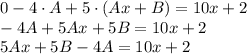
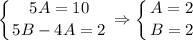
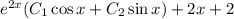
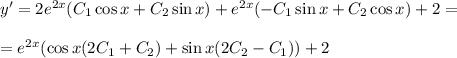
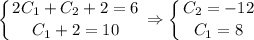
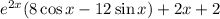
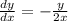
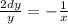 - уравнение с разделёнными переменными
- уравнение с разделёнными переменными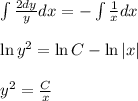
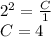
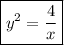 - частный интеграл.
- частный интеграл.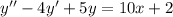
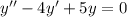
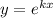 , тогда получаем
, тогда получаем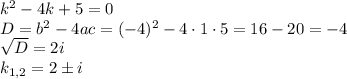
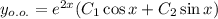
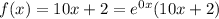
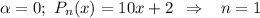
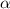 с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде:
с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде: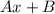
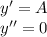
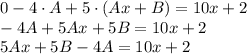
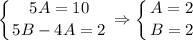
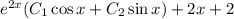
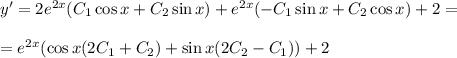
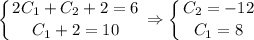
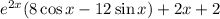
2) Wo warst du gestern? - Wir waren im Zirkus.
3) Gehst du ins Museum oft? - Nein, nicht sehr oft.
4) Möchtest du am Sonntag in die Disko gehen? - Nein, ich fahre mit den Eltern zu meiner Oma.
5) Ist Tanja da? - Nein, sie ist mit dem Hund in den Park gegangen.
6) Ich möchte in die Galerie gehen. Kommst du mit?
7) Ich habe Hunger. Gehen wir mal ins Café!
8) Wart ihr im Kino? - Ja, wir haben einen neuen Film gesehen.