1) 100%-10%=90% от вторичной цены становят 540р
2) 540:90*100=600 р - вторичная цена
3) 100%-20%=80% от первоначальной цены становят 600 р
4) 600:80*100=750 р - первоначальная цена
ответ: 750р
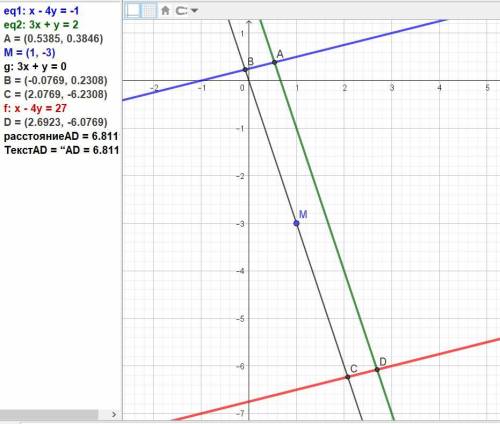
Уравнение прямой, включающей сторону ВС, найдём, подставив координаты точки М в уравнение с координатами переменных, как у параллельной прямой AD 3x + y – 2 = 0.
3*1 + (-3) + C = 0, отсюда С = -3 + 3 = 0.
Получаем уравнение BC: 3x + y = 0.
Находим вершину B параллелограмма как точку пересечения прямых АВ и ВС, решив систему:
{x – 4y + 1 = 0 x – 4y + 1 = 0
{3x + y = 0 (x4) = 12x + 4y = 0
13x + 1 = 0, x = -1/13,
y = – 3x = – 3(-1/13) = 3/13. Точка В((-1/13); (3/13)).
Находим точку С как симметричную точке В относительно точки М(1; -3).
х(С) = 2х(М) – х(В) = 2*1 - (-1/13) = 27/13,
y(С) = 2y(М) – y(В) = 2*(-3) - (3/13) = -81/13.
Уравнение прямой, включающей сторону CD, найдём, подставив координаты точки C в уравнение с координатами переменных, как у параллельной прямой AB x - 4y + 1 = 0.
(27/13) - 4(-81/13) + C = 0, отсюда С = (-27/13) – (324/13) = -351/13 = -27.
Получаем уравнение CD: x - 4y - 27 = 0.
пусть х(руб)-первоначальная цена товара, после снижения на 20%, товар стоил 0,8х(руб), а после снижения еще на 10%, он стал стоить 0,72х(руб), что составляет 540(руб). Составим и решим уравнение:
0,72х=540,
х=540:0,72
х=750
750(руб)-первоначальная цена товара.
ответ:750 руб.