Целая часть числа — График целой части В математике, целая часть, антье (фр. entier) или функция «пол» (англ. floor) это функция, определённая на множестве вещественных чисел и принимающая целочисленные значения. Целая часть числа x обычно обозначается через или [x]
целая часть числа - это наибольшее целое число , удовлетворяющее неравенству , то есть наибольшее целое число, не превосходящее . По предложению Гаусса, эта фунция обозначается как .
Заметим, что для отрицательных чисел понятие целой части не совсем согласуется со здравым смыслом.
36
Пошаговое объяснение:
Спортсмены бегают по некому пути, который можно представить в виде прямой. Все спортсмены пробегают одинаковое расстояние (далее — S), но с разной скоростью. Обозначим скорости Андрея — a, Бори — b, Васи — v. Т. к. мы уже выяснили, что спортсмены бегают по окружности, а её можно представить как прямую, то можно составить следующую систему:
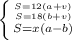
Выразим a и b:
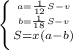
Далее применим метод подстановки:
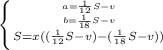
Затем рассматриваю лишь последнее уравнение системы. Раскрываем скобки.
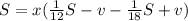
Убираем противоположные.
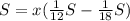
Считаем значения в скобках. Умножаем скобку на x.
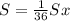
Получаем:

Чтобы умножить число на сумму чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить. Отсюда равенства:
(3 + 9 + 5) * 2 = 3 * 2 + 9 * 2 + 5 * 2 (= 34)
(2 + 7 + 4) * 3 = 2 * 3 + 7 * 3 + 4 * 3 (= 39)
(8 + 4 + 6) * 4 = 8 * 4 + 4 * 4 + 6 * 4 (= 72)
№2.
(9 + 4 + 2) * 5 = 9 * 5 + 4 * 5 + 2 * 5 (= 75)
(3 + 8 + 5) * 6 = 3 * 6 + 8 * 6 + 5 * 6 (= 96)