Улитка пытается залезть на столб 20 м высотой на какой день она доползёт до верха если за дент улитка поднимается на 9 м а за ночь спускается на 4 м

👇

Увидеть ответ

Ответ:

davidgts

08.02.2022

9-4=5м поднимается за сутки
20:5=4 суток

4,5(86 оценок)

Открыть все ответы

Ответ:

сел5

08.02.2022

Zadanie 4 (Задание 4)

Найдите количество деревьев на n вершинах, в которых степень каждой вершины не больше 2.

n=1 => дерево состоит из одной вершины степени 0.

n>=2 => 1] Вершины степени 0 быть не может (иначе граф несвязный). Значит степень вершин либо 1, либо 2. 2] существует простая цепь, являющаяся подграфом дерева.

Тогда будем достраивать дерево из цепи. Ребро - простая цепь.

Алгоритм:

Изначально есть ребро <u,v>. Степени концов цепи - вершин u и v - равны 1.

Если на данном шаге число вершин в графе равно n - получен один из искомых графов, больше его не изменяем.

Если же число вершин < n, добавляем ребро.

На 1ом шаге мы можем добавить либо ребро <u,a>, либо ребро <a,v>. Без нарушения общности, добавим <u,a>. У нас все еще простая цепь. При этом у концов a и v степень 1, а у всех остальных вершин, здесь это вершина u, - 2, и к ним ребра присоединить уже нельзя. Повторяя подобные операции, будем получать на каждом шаге простую цепь.

На n вершинах можно построить ровно одну простую цепь. А значит и число искомых деревьев равно 1 .

Zadanie 5 (Задание 5)

Покажите, что для графа G=[V,E] с k компонентами связности верно неравенство $|V|-k\leq |E|\leq \left(\begin{array}{c}|V|-k\\2\end{array}\right)$

Введем обозначения |V|=n, |E|=m

Разобьем граф на компоненты связности. Для каждой компоненты, очевидно, верно неравенство 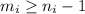$m_i\geq n_i-1$ . Просуммировав неравенства для каждой из k компонент, получим $m\geq n-k$ .

Оценка снизу получена.

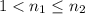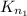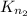Лемма: Граф имеет максимальное число ребер, если он имеет k-1 тривиальную компоненту связности и 1 компоненту, являющуюся полным графом. И действительно. Пусть $K_{n_1}, K_{n_2}$ – компоненты связности, . Тогда при "переносе" одной вершины из $K_{n_1}$ в $K_{n_2}$ число ребер увеличится на 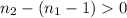n_2-(n_1-1)0 – а значит такая "конфигурация" неоптимальная, и несколькими преобразованиями сводится к указанной в лемме. А тогда максимальное число ребер в графе равно 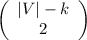$\left(\begin{array}{c}|V|-k\\2\end{array}\right)$ Оценка сверху получена.

Zadanie 6 (Задание 6)

Проверьте, являются ли следующие последовательности графическими, обоснуйте ответ

Решение в приложении к ответу

Плата Очень нужна математика дискретная Задание 4).Найдите количество деревьев с n вершинами, в кото

4,4(69 оценок)

Ответ:

KoteikaOneLove

08.02.2022

Мосвязи, возможности и пути синтеза музыки и архитектуры.В истории художественной культуры архитектура и музыка не связаны между собой столь тесно, как, например, архитектура и скульптура, архитектура и живопись, музыка и поэзия и др. И вместе с тем между архитектурой и музыкой возникают определенные формы взаимосвязи, существенные и для теории, и для художественной практики. Янис Ксенакис, один из ведущих композиторов второй половины XX века, на примере своего творчества блестяще проиллюстрировал возможности симбиоза музыки и архитектуры:«Хотим мы этого или нет, между архитектурой и музыкой существует мостик» Общеизвестно, что Аристотель видит в изобразительных искусствах подражание или род знания. Воззрение это лежало в самом существе художественной культуры древних греков. Однако в данном случае для нас гораздо интереснее то, что этот взгляд Аристотель распространяет и на искусство музыки и поэзии. И в этих искусствах он видит искусства «подражательные».Более того, по мнению Аристотеля, область подражания, доступная музыке, в известном отношении шире области, составляющей удел пластики и живописи. Изобразительную силу музыки.Аристотель оценивал чрезвычайно высоко. Действие,воспроизводимое музыкой нравственного характера или состояния,настолько сильно, что чувство, возбужденное в нас музыкальным изображением, может переноситься на реальных людей, характеры которых изображаются мелодией. «Кто, например, глядя на чье-либо изображение, испытывает радостное чувство не по какой-либо другой причине, а именно из-за данного внешнего образа, тому, конечно,приятно будет и встретиться лицом к лицу с человеком, на чье изображение он смотрит.Эту же мысль доказывает и А. Г. Габричевский, крупнейший деятель русской культуры, чья личность и творчество повлияли на интеллектуальную жизнь нашей страны в XX веке: «...грань между искусством пространственным и временным чрезвычайно зыбка». Можно выделить некоторые формы такой взаимосвязи.1. Генетическая общность многих конкретно-исторических явлений двух данных искусств, обусловленная их происхождение одной социальной основы. Отсюда – образная и стилистическая близость музыки и архитектуры в определенные периоды культурного развития, что позволяет выявить аналогии между кругом идей,образов и выразительных средств. В музыке прослеживается отражение картинности, объемности (особенно в программной музыке), мы можем «видеть» море, замок, парад, а в архитектуре –отражение категории музыкальности. При создании архитектурного объекта звучание музыкальных инструментов часто предопределяет само архитектурное решение.

4,6(26 оценок)

Это интересно:

Образование-и-коммуникации

23.07.2020

Как определить медиану множества: ключевые понятия и методы расчёта...

Дом-и-сад

17.04.2023

Как правильно покрасить древесину: советы от профессионалов...

Путешествия

23.02.2023

Как развить туристический бизнес: советы от экспертов...

Образование-и-коммуникации