Вариант 1:
основное свойство пропорции (6 класс математика)
если a : b = c : d, то a x d = c x b
для нашего случая получим:
5,6 х 3 = 0,4 х (3х + 12)
16,8 = 1,2х + 4,8
1,2х = 16,8 - 4,8
1,2х = 12
х = 12 : 1,2
х = 10
Вариант 2:
5,6 = 0,4 х 14
3х + 12 = 3 х (х + 4)
< var > \frac{0,4}{3} = \frac{0,4 \cdot 14}{3 \cdot (x+4)} < /var ><var>
3
0,4
=
3⋅(x+4)
0,4⋅14
</var>
это возможно только тогда, когда
< var > \frac{14}{(x+4)} = 1 < /var ><var>
(x+4)
14
=1</var>
получается, что числитель и знаменатель равны
14 = х + 4
х = 14 - 4
х = 10
Пошаговое объяснение:
перепишем уравнение заданной прямой в виде y = kx+b
2y+x +3 = 0
y = -0.5x -1.5
отсюда мы найдем коэффициент наклона нашей нормали. т.к. нормаль должна быть ║ заданной прямой, то и угловые коэффициенты у них должны быть равными.
т.о. угловой коэффициент наклона нормали = -0,5
уравнение нормали
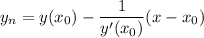
теперь надо найти точку кривой, в которой
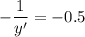

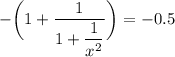
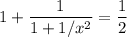
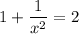
отсюда получим х = ± 1
т.е. у нас есть две точки с абсциссами х=1 и х = -1, принадлежащие кривой у= х -1/х, удовлетворяющие нашим условиям построения нормали
две точки потому, что график функции у = х -1/х состоит из двух кривых
теперь для нормали в виде у = kx+b у нас есть x. найдем у и b
у(1) = 0 0=-0,5*1+b b= 0.5
уравнение нормали у = -0,5х +0,5
у(-1) = 0 0= -0,5*(-1)+b b = -0.5
уравнение нормали у = -0,5х -0,5
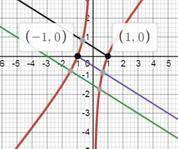
на графике
красным у = х -1/х
зеленым 2у+х+3 = 0
фиолетовым и зеленым - две нормали. специально их укоротила, чтобы было видно к какой дуге кривой относится каждая нормаль
х+286=315+232
х+286=547
х=547-286
х=261 чел- во вторник
261+286+315+232=1094 чел всего