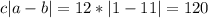Решение перебором.
Пусть число имеет вид , где - сотни, - десятки и - единицы. Для начала будем считать, что (просто потому, что числа с условием получаются автоматически "переворачиванием" тех, что мы найдем сначала). Возможны следующие случаи - , тогда или . (поскольку и должны быть натуральными числами) Это дает нам числа 124 и 139. Кроме того, можно заметить (подобное замечание было уже однажды сделано выше по тексты), что числа 421 и 931 тоже подходят. Более того, число 421 удовлетворяет и второму условию задачи, и третьему. Если к цифрам 4, 2, 1 прибавить 8, 5, 1, то получим числа 12, 7, 2. Эти последние действительно образуют арифметическую прогрессию с разностью .
Второй возможный случай . Тогда и других возможностей нет. В этом случае и , что дает нам числа 248 и 842. Оба эти числа не подходят под условия задачи.
120
Пошаговое объяснение:
Пусть Саша выбрал число a, Андрей - число b, Оля - число c. Опишем последовательность действий.
1) Саша умножил своё число на каждое из других, получилось ab и ac. Затем вычел меньшее из большего. Тогда получается выражение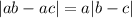
. a можно вынести за модуль, так как оно натуральное.
2) Аналогично, у Андрея получилось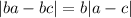
.
У Оли получилось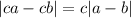
3) По условию,
Из первого равенства можно получить два варианта:
а)
б)
поскольку 1 можно разложить на натуральные множители лишь
Рассмотрим второе равенство и подставим туда каждый случай из первого:
а)
Отсюда:
б)
Отсюда:
Далее находим c: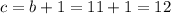
Однозначно определяем число Оли: