Пошаговое объяснение:
4) члены геометрической прогрессии
b₁=3к-2
b₂=2к
b₃=к+3
а)
мы знаем, что отношение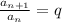 
, составим такие отношения
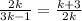⇒ 4k² = (3k-1)(k+3) ⇒ k²-7k+6 =0 ⇒ k₁ = 1; k₂ = 6
b) теперь строим прогрессии
для k₁ = 1 : b₁=3*1-2=1; b₂=2*1=2; b₃=1+3= 4 это возрастающая прогресстя
для k₂ = 6 b₁=3*6-2=16; b₂=2*6=12; b₃=6+3= 9 - это бесконечно убывающая геометрическая прогрессия, ее сумма
, у нас b₁= 16, найдем q= b₂/b₁= 12/16= 0.75, тогда
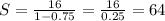
5.
рассуждаем так, в каждом последующем ряду бревен будет на 1 меньше, тогда n-член арифметической прогрессии имеет вид
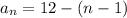, посмотрим, какой ряд будет последним (будет иметь одно бревно)
12-(n-1)=1 ⇒ n=12
найдем сумму 12 членов арифметической прогрессии
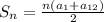
Последние три буквы НУЛ при умножении на 5 остаются. Это может быть только 250 или 750.
1) 250*5=1250
Рассмотрим три старших разряда.
(100*Ш+10*Е+П)*5+1= 1000*К+100*Р+10*И+К
К-1 должно делиться на 5. Значит, К=1 или 6. Но 9*5=45, значит, К не может быть больше 4. То есть К=1, Ш=3. Тогда П должно быть четным. Буквы Е, И, Р могут быть какими угодно, но нужно подобрать так, чтобы цифры не повторялись. Проверка показывает, что ни один вариант не подходит.
2) 750*5=3750
(100*Ш+10*Е+П)*5+3=1000*К+100*Р+10*И+К
К=3; Ш=6; П - чётное.
Проверка даёт два решения:
628750*5=3143750
682750*5=3413750