ответ:
отложим одну монету, а на каждую чашу весов положим по две монеты. возможны два случая.
1) весы в равновесии. так как четырёх настоящих монет нет, то на одной чаше лежат обе фальшивые монеты. следующим взвешиванием достаточно сравнить веса монет с одной чаши: если весы в равновесии, то эти монеты настоящие, и фальшивые монеты в другой чаше; если весы не в равновесии, то фальшивые монеты – на весах.
2) одна из чаш перевесила. тогда на весах находится или только лёгкая фальшивая монета в более лёгкой чаше или только тяжёлая фальшивая монета в более тяжёлой чаше, или обе монеты находятся в разных чашах. вторым взвешиванием сравним веса монет в лёгкой чаше: если весы не в равновесии, то более лёгкая монета – фальшивая. если весы в равновесии, то отложенная монета – фальшивая (и она лёгкая). аналогично, третьим взвешиванием сравним веса монет из тяжёлой чаши: тогда, либо более тяжёлая монета – фальшивая, либо, если весы в равновесии, отложенная монета фальшивая (и она тяжёлая).
решение 2
первый раз положим на чаши весов первую и вторую монеты, а второй раз – третью и четвёртую. возможны только два случая.
1) один раз весы были в равновесии (пусть при первом взвешивании; при этом на чашах настоящие монеты), а другой раз – нет.
возьмем настоящую монету из первого взвешивания и сравним её с той, что оставалась на столе. если их веса равны, то последняя монета настоящая, а фальшивые – те, что участвовали во втором взвешивании. иначе, монета со стола – фальшивая, и мы знаем, легче она настоящей или тяжелее, а потому знаем, лёгкая или тяжёлая фальшивая монета участвовала во втором взвешивании.
2) оба раза весы были не в равновесии. тогда на весах каждый раз была одна фальшивая монета, а на столе осталась настоящая. взвесим её с лёгкой монетой из первого взвешивания. если веса равны, то в первом взвешивании фальшивой была более тяжёлая, а во втором – более лёгкая. если же более лёгкая монета из первого взвешивания оказалась легче, то она фальшивая, а из второго взвешивания фальшивая – более тяжёлая.
замечания
отметим, что решение 2 не использует то, что обе фальшивых монеты весят столько же, сколько две настоящих.
Зауважимо, що якщо всі частини будуть прямокутної форми, то максимальна кількість частин, на які розрізаний квадрат, дорівнює 18. Це випливає з того, що якщо розрізати квадрат на прямокутники зі сторонами 1×2, то ми отримаємо 32 частини, а якщо на прямокутники зі сторонами 1×1, то ми отримаємо 16 частин.
Оскільки не всі частини повинні бути прямокутних, то можна розглянути дві такі частини, які мають різний периметр і обидві не є прямокутними.
Зафіксуємо пряму лінію, яка фактично розрізає квадрат на дві частини. Тоді можна помітити, що можливі три варіанти для форми однієї з частин: прямокутник, трикутник або багатокутник з більш ніж чотирма вершинами.
Якщо одна з частин має прямокутну форму, то максимальна кількість частин буде такою ж, як у випадку прямокутних частин. Якщо одна з частин має форму трикутника, то інша частина повинна складатися з двох трикутників або бути більш ніж чотирьохкутником. У першому випадку ми отримуємо три частини, у другому - п'ять. Якщо одна з частин має форму більш ніж чотирьохкутника, то інша частина повинна бути менш ніж чотирьохкутником і ми отримуємо як мінімум дві частини.
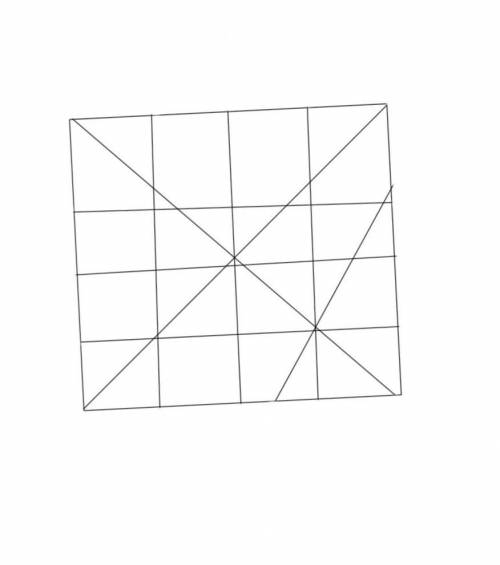
Отже, максимальна кількість частин, яку можна отримати при розрізанні квадрата на частини однакового периметра з урахуванням можливості не прямокутної форми частин, дорівнює 21. Одне з можливих розбиттів наведено на малюнку нижче.
Площа: 16 дм²
3*4=12 =>
12*2=24