высота=8см, S∆AOB=S∆BOC=S∆COD=S∆AOD=64см²
Пошаговое объяснение:
диагонали квадрата делят его на 4 равных равнобедренных прямоугольных треугольника, в которых стороны квадрата - гипотенузы, а диагонали - катеты. Обозначим вершины квадрата В С Д с диагоналями АС и ВД а точку их пересечения О. Проведём высоту ∆ВОС и АОД. Она равна ВК равна стороне квадрата и поскольку его диагонали при пересечении делятся пополам, то КО=ОН=½×АВ=½×16=8см
Поскольку треугольники равны, то величина высоты у всех будет одинаковая
Итак: высота каждого треугольника составляет 8см
У равнобедренного прямоугольного треугольника катеты меньше гипотенузы в √2 раз, поэтому АО=СО=ВО=ДО=16/√2=8√2см (если 16 разложить как 8×√2×√2/√2=8√2)
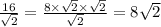
Площадь прямоугольного треугольника вычисляется по формуле:
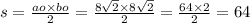
Итак: S=64см²
Диагонали квадрата пересекаются под прямым углом и поэтому Эти треугольники, на которые диагонали делят квадрат являются прямоугольными равнобедренными, и диагонали делятся пополам на равные части и являются катетами в этих треугольниках, которые меньше гипотенузы в √2 раз,. а углы, прилегающие к гипотенузе равны каждый по 45°.
1) 3·x > -18
x > -18:3
x > -6
x∈(-6; +∞)
2) -8·x < 32
x > 32:(-8) (так как делим на отрицательное число)
x > -4
x∈(-4; +∞)
3) x+5 > -3
x > -3-5
x > -8
x∈(-8; +∞)
4) 6,5·y > 13
x > 13:6,5
x > 2
x∈(2; +∞)
5) -8·x > 24
x < 24:(-8) (так как делим на отрицательное число)
x < -3
x∈(-∞; -3)
6) 7,5·x < 30
x < 30:7,5
x < 4
x∈(-∞; 4)