1) В произведении от 1 до 100 есть 9 чисел, оканчивающихся 0 (10,20,30,40,50,60,70,80,90), и число 100 с двумя нулями.
2) Кроме того 5 · 2 = 10
Каждое умножение 5 и 2 даст на конце 0. Числа, которые оканчиваются на 5 : 5,15,25,35,45,55,65,75,85,95 - всего 10 чисел.
3) Числа, которые имеют по два множителя 5 : 25,50,75 - всего 3.
От 1 до 100 есть 9+2=11 нулей и ещё 10+3=13 пятёрок, для которых найдётся нужное количество двоек, например
64 · 32 · 4 = 2⁶ · 2⁵ · 2² = 2¹³
11 + 13 = 24
ответ : 24 нуля
ответ:
да
пошаговое объяснение:
поскольку 1^3 + 2^3 + 3^3 = 36 делится на 9, то для n = 1 утверждение верно.
предположим, что оно верно для n = k, то есть k^3 + (k + 1)^3 + (k + 2)^3 = 9m для некоторого натурального числа m. нам нужно доказать для n = k + 1.
но действительно,
(k + 1)^3 + (k + 2)^3 + (k + 3)^3 = (k + 1)^3 + (k + 2)^3 + k^3 + 27k + 9k2 + 27 =
= 9m + 27k + 9k2 + 27 = 9(m + 3k + k2 + 3)
делится на 9, и мы заключаем, что утверждение верно для любого n.
ответ:29
Пошаговое объяснение:
Задача
Мам - 12
Малышей - ? на 5 м чем (рисуем стрелочку на верх к мамам)
Постарше - ? на 3 б чем (рисуем стрелочку к малышам)
(Все берем в фигурную скобку }и ставим знак -? )
Объясните решению
Сначала нам нужно найти сколько у нас малышей, малышей у нас на 5 меньше чем мам, а значит мы от 12 отнимает 5.
1) 12-5= 7 (м)
Теперь нам нужно найти второе не известное (старших детей) мы уже знаем что младших детей у на 7 а старших на 3 ребенка больше чем меньших, в итоге получается
2) 7+3=10 (ст.д)
Теперь мы находим третье не известное, это общее количество мам и детей
3) 12+7+10=29 (ч)
1) 12 - 5 = 7 (м.д)
2) 7 + 3 =10 (ст.д)
3) 12 + 7 + 10= 29
ответ 29 ч
Подсчитаем сколько раз приходится число 2 в факториал 100
В разложении на простые множители числа 100! двойка встречается ровно 97 раз.
Теперь подсчитаем сколько раз приходится число 5 в факториал 100
Число 5 встречается ровно 24 раза.
Значит,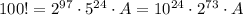 , где А - некоторый множитель. И как видим, данное произведение оканчивается 24 нулями.
, где А - некоторый множитель. И как видим, данное произведение оканчивается 24 нулями.
ответ: 24 нулями.