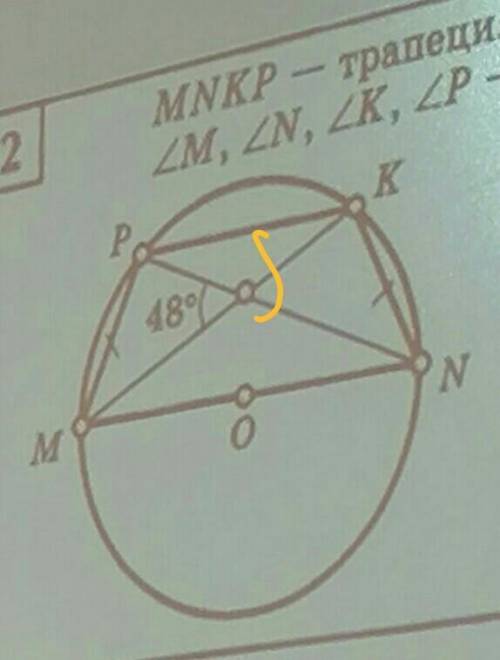
Угол MPN= 90°,т.к опирается на диаметр MN.
Рассматривая треугольник MPS, где угол MPS=90°, угол MSP=48°, следовательно угол PMS= 42°.
Угол KSN=PSM(как вертикальные)
Угол MKN=MPN(т.к опираются на MN.
Значит, угол KNP=42°.
Угол MSN= 180°-угол PSM= 180°-48= 132°
MS=SN( в равнобедренной трапеции диагонали делятся точкой пересечения на попарно равные отрезки)=> треугольник MSN - равнобедренный.
угол SMN+угол SNM= 180°- угол MSN= 180°-132°=48°
угол SMN=углу SNM= 48°/2= 24°
Следовательно угол М=угол PMS+ угол SMN= 42°+24°= 66°
Угол N=углу М= 66°(т.к равнобедренная трапеция)
Угол P= 180°- угол М= 114°
Угол К= углу P= 114°.
ответ: Угол М,N= 66°; угол P,K= 114°.
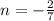 - знаменатель обращается в 0.
- знаменатель обращается в 0.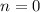 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)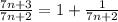

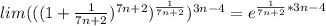 (при
(при  →∞)
→∞)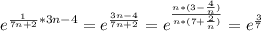 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→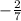
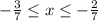 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
2)0,02/0,0005=40
3)0,7/0,0014=500
4)1000+40=1040
5)1040-500=540