Question

Через две трубы бассейн наполняется за 6 часов, причем через одну трубу наполняется весь бассейн на 5 часов быстрее, чем через вторую. за сколько часов наполняется бассейн через каждую трубу в отдельности?

Answer 1

Допустим полный бассейн = 1. Если первая труба наполняет бассейн в х ч, то вторая наполняет его в ( х + 5 ) ч

Составляем уравнение:

1) $\frac{1}{x}+\frac{1}{x+5}=\frac{1}{6}$

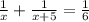
2) $\frac{2x+5}{x^{2}+5x}=\frac{1}{6}$ 

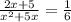
3) $12*x+30={x^{2}+5*x$ 

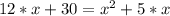
4) ${x^{2}-7*x-30=0$ 

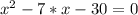
5) $D = {(-7)^{2} - 4*1*(-30) = 169$ 

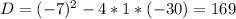
  x1 = 10

  x2 = -3

x1 - верно

x2 - не верно

находим время наполнения бассейна второй трубой:

10+5=15ч

ответ: первая труба наполнит бассеин за 10ч вторая труба за 15ч