Математика: Решите уравнение 0.6*(y-3)-0.5*(y-1)=1.5

1. Уравнение гиперболы имеет стандартный вид: , где а и b - полуоси гиперболы Значит, у гиперболы Правый фокус гиперболы имеет вид F(c; 0), где Находим с: Так как окружность проходит через начало координат, то ее радиус равен абсциссе правого фокуса, то есть Общий вид уравнения окружности: , где - центр окружности, R - ее радиус Уравнение окружности: Асимптоты гиперболы имеют вид: Тогда, асимптоты гиперболы Подставляем в уравнение окружности выражение для у: Тогда у для соответствующих х равны:...

Решите уравнение 0.6(y-3)-0.5(y-1)=1.5

👇

Увидеть ответ

Ответ:

TanyaCat225

02.08.2021

0,6(у-3)-0,5(у-1)=1,5
0,6у-1,8-0,5у+0,5=1,5
0,1у=2,8
у=28

ответ:у =28

4,4(64 оценок)

Ответ:

lalka20022

02.08.2021

0,6y-0,6*3 -0,5y +0,5 = 1,5
0,1y = 1,5-0,5+1,8
0,1y = 2,8
y = 2,8/0,1
y =28

4,6(22 оценок)

Открыть все ответы

Ответ:

RUMBANITTA

02.08.2021

Відповідь:

0,09 = 9%

1,7 = 170%

0,3 = 30%

0,5 = 50%

0,25 = 25%

0,14 = 14%

2 = 200%

6% = 0,06

13% = 0,13

22% = 0,22

50% = 0,5

67% = 0,67

230% = 2,3

400% = 4

3/4 = 75%

2/5 = 20%

1/2 = 50%

4/5 = 80%

1/20 = 5%

13/50 = 26%

2,0928 + 47,9072 : ( 7 - 0,195 ) = 9,13

1) 7 - 0,195 = 6,805

2) 47,9072 : 6,805 = 7,04

3) 2,0928 + 7,04 = 9,13

Покрокове пояснення:

1. Добавляешь к каждому числу два нуля.

Пример: 0,09 + ,00 = 9%.

2. Действие противоположное первому пункту.

3. Делишь 100% на ( пример ) 4 части, т.е

3/4

Берёшь 4 и делишь на это число 100%.

100/4 = 25

Теперь берёшь 3 и множишь на то, что получилось после деления 100%, т.е 25

3*25 = 75%.

4,7(48 оценок)

Ответ:

sergejryazanov228

02.08.2021

1.
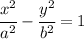Уравнение гиперболы имеет стандартный вид: $\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} =1$ , где а и b - полуоси гиперболы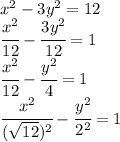
$x^2-3y^2=12 
\\\
 \cfrac{x^2}{12} - \cfrac{3y^2}{12} =1
\\\
 \cfrac{x^2}{12} - \cfrac{y^2}{4} =1
\\\
 \cfrac{x^2}{( \sqrt{12} )^2} - \cfrac{y^2}{2^2} =1$
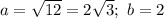
Значит, у гиперболы $a= \sqrt{12} =2 \sqrt{3} ;\ b=2$
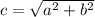
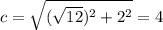
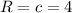
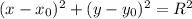Правый фокус гиперболы имеет вид F(c; 0), где $c= \sqrt{a^2+b^2}$
Находим с:
$c= \sqrt{( \sqrt{12})^2+2^2 } =4$
Так как окружность проходит через начало координат, то ее радиус равен абсциссе правого фокуса, то есть R=c=4

Общий вид уравнения окружности: (x-x_0)^2+(y-y_0)^2=R^2

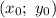, где $(x_0; \ y_0)$ - центр окружности, R - ее радиус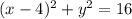
Уравнение окружности: (x-4)^2+y^2=16

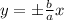
Асимптоты гиперболы имеют вид: $y=\pm \frac{b}{a} x$
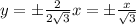
Тогда, асимптоты гиперболы $y=\pm \frac{2}{2 \sqrt{3} } x=\pm\frac{ x }{\sqrt{3}}$
Подставляем в уравнение окружности выражение для у:
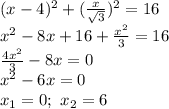
$(x-4)^2+( \frac{x}{ \sqrt{3} } )^2=16
\\\
x^2-8x+16+ \frac{x^2}{ 3} } =16
\\\
 \frac{4x^2}{ 3} }-8x =0
\\\
x^2-6x =0
\\\
x_1=0; \ x_2=6$
Тогда у для соответствующих х равны:
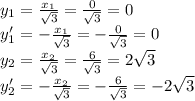
$y_1= \frac{x_1}{ \sqrt{3} } =\frac{0}{ \sqrt{3} } =0 \\\ y_1'= -\frac{x_1}{ \sqrt{3} } =-\frac{0}{ \sqrt{3} } =0 \\\ y_2= \frac{x_2}{ \sqrt{3} } =\frac{6}{ \sqrt{3} } =2 \sqrt{3} 
\\\
y_2'= -\frac{x_2}{ \sqrt{3} } =-\frac{6}{ \sqrt{3} } =-2 \sqrt{3}$
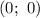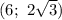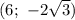
ответ: $(0; \ 0)$ ; $(6; \ 2 \sqrt{3} )$ ; $(6; \ -2 \sqrt{3} )$

2.
Так как известна одна полуось и точка, принадлежащая гиперболе, о можно найти вторую полуось:
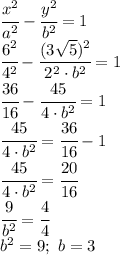
$\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} =1
\\\
 \cfrac{6^2}{4^2} - \cfrac{(3 \sqrt{5}) ^2}{2^2\cdot b^2} =1
\\\
 \cfrac{36}{16} - \cfrac{45}{4\cdot b^2} =1
\\\
 \cfrac{45}{4\cdot b^2} = \cfrac{36}{16}-1
\\\
 \cfrac{45}{4\cdot b^2} = \cfrac{20}{16}
\\\
 \cfrac{9}{b^2} = \cfrac{4}{4}
\\\
b^2=9; \ b=3$
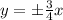
Тогда уравнения асимптот принимают вид: $y=\pm \frac{3}{4} x$
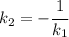
Угловой коэффициент перпендикулярной прямой является обратным и противоположным числом к угловому коэффициенту исходной прямой: $k_2=- \cfrac{1}{k_1}$
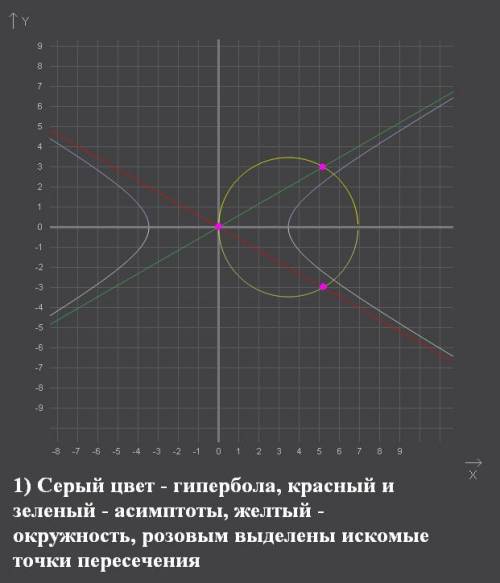
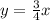Тогда, для прямой $y=\frac{3}{4}x$ таким коэффициентом является число 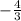$- \frac{4}{3}$ , а для прямой 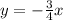$y=-\frac{3}{4}x$ - число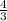 $\frac{4}{3}$
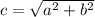
Левый фокус гиперболы имеет вид F(-c; 0), где $c= \sqrt{a^2+b^2}$
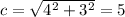$c=\sqrt{4^2+3^2} =5$ , следовательно через точку (-5; 0) нужно провести искомые прямые
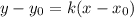
Уравнение прямой, проходящей через заданную точку $(x_0; \ y_0)$ с заданным угловым коэффициентом k имеет вид: y-y_0=k(x-x_0)

Тогда:
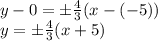
$y-0=\pm \frac{4}{3} (x-(-5))
\\\
y=\pm \frac{4}{3} (x+5)$
Или по отдельности:
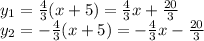
$y_1=\frac{4}{3} (x+5)=\frac{4}{3} x+ \frac{20}{3} 
\\\
y_2=-\frac{4}{3} (x+5)=-\frac{4}{3} x- \frac{20}{3}$

№1. найти точки пересечения асимптот гиперболы х²-3у²=12 с окружностью,имеющей центр в правом фокусе