Математика: По договору можно работать и с 15 лет

По договору можно работать и с 15 лет

👇

Увидеть ответ

Ответ:

AlionaNigrevskaya

02.01.2020

Работать не более 4 часов в день
И ещё надо письменное согласие родителей

4,5(47 оценок)

Открыть все ответы

Ответ:

Anna124212

02.01.2020

Вероятность события "монета выпала решкой ровно 10 раз" больше вероятности события "монета выпала решкой ровно 13 раз" в 14,3 раза.

Объяснение:

Определить, во сколько раз вероятность события "монета выпала решкой ровно 10 раз" больше вероятности события "монета выпала решкой ровно 13 раз".

1) Введем обозначения по условию:

Число бросков n = 16:

1-е событие "монета выпала решкой ровно 10 раз" k = 10;

2-е событие "монета выпала решкой ровно 13 раз" k = 13.

Найти отношение вероятности первого события ко второму:

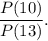
$\displaystyle \frac {P(10)}{P(13)}.$

Вероятностью наступления некоторого события называется отношение числа благоприятных исходов к числу всех возможных исходов.

2) При бросании монеты число всех исходов равно 2ⁿ.

В нашем случае число всех возможных исходов одной или другой стороны монеты при 16 бросках равно 2¹⁶.

Число сочетаний без повторений из n элементов по k - это количество , которыми можно выбрать k элементов из n без учета порядка.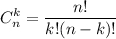

$\displaystyle C^{k} _{n} = \frac{n!}{k! (n-k)!}$

3) Число благоприятных исходов в первом случае.

Число бросков n = 16

Число выпадений решки k = 10.

Число благоприятных исходов в первом случае равно числу сочетаний из 16 по 10.

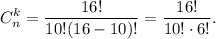
$\displaystyle C^{k} _{n} = \frac{16!}{10! (16-10)!}= \frac{16!}{10! \cdot 6!}.$

4) Вероятность события "монета выпала решкой ровно 10 раз".

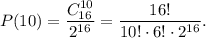
$\displaystyle P(10) = \frac{C^{10}_{16}}{2^{16}} = \frac{16!}{10! \cdot 6! \cdot 2^{16} } .$

5) Число благоприятных исходов во втором случае.

Число бросков n = 16

Число выпадений решки k = 13.

Число благоприятных исходов во втором случае равно числу сочетаний из 16 по 13.

$\displaystyle C^{k} _{n} = \frac{16!}{13! (16-13)!}= \frac{16!}{13! \cdot 3!}.$

6) Вероятность события "монета выпала решкой ровно 13 раз"

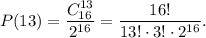
$\displaystyle P(13) = \frac{C^{13}_{16}}{2^{16}} = \frac{16!}{13! \cdot 3! \cdot 2^{16} } .$

7) Найдем, во сколько раз вероятность первого события больше вероятности второго события.

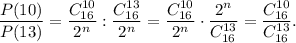
$\displaystyle \frac{P(10)}{P(13)} =\frac{C^{10}_{16}}{2^{n}} : \frac{C^{13}_{16}}{2^{n}} =\frac{C^{10}_{16}}{2^{n}} \cdot \frac{2^{n}}{C^{13}_{16}} =\frac{C^{10}_{16}}{C^{13}_{16}} .$

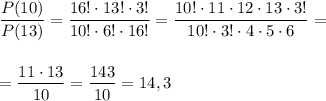
$\displaystyle \frac{P(10)}{P(13)} =\frac{16! \cdot 13! \cdot 3!}{10! \cdot 6! \cdot 16!} =\frac{10! \cdot 11 \cdot 12 \cdot 13 \cdot 3!}{10! \cdot 3! \cdot 4 \cdot 5 \cdot 6} =\\\\\\=\frac{11 \cdot 13}{10} = \frac{143}{10} =14,3$

4,8(100 оценок)

Ответ:

1234fghh

02.01.2020

б) 7ц3/8+1ц7/10=7ц 3*5/8*5 + 1ц 7*4/10*4=7ц15/40 + 1ц28/40=8ц 43/40=9ц 3/40
в) 4ц11/12+5ц13/18=4ц11*3/12*3 + 5ц 13*2/18*2= 4ц33/36 + 5ц26/36= =9ц59/36=10ц 23/36
г) 9ц2/9-6ц5/6=9ц2*2/9*2 - 6ц5*3/6*3=9ц4/18 - 6ц15/18=8ц18/18+4/18 -6ц15/18= 8ц22/18 - 6ц15/18=2ц7/18

уравнения:
а) b+5ц9/10=7ц5/12
b=7ц5/12-5ц9/10
b=7ц5*5/12*5 - 5ц9*6/10*6
b=7ц25/60 - 5ц54/60
b=6ц+60/60+25/60 - 5ц54/60
b=6ц+85/60 - 5ц54/60
b=1ц31/60

б) 3,85*(d-4,02 )=8,47
d-4,02 =8,47: 3,85
d-4,02 =2,2
d =2,2+4,02
d =6,22
проверка
3,85*(6,22-4,02)=8,47
3,85*2,2=8,47
8,47=8,47
последнее задание сейчас соображу и допишу

4,7(73 оценок)

Это интересно:

Образование

06.01.2021

Клюква стоит 250 рублей за кг, а малина 200....

Образование

16.03.2023

Решить систему уравнений x2 + y2 + xy = 3...

Образование

05.08.2020

Решить систему уравнений x2 + xy +y2 = 13...

Образование