на плоскости:
1) пролегает мимо окружности
2) пролегает через центр окружности
3) прямая имеет 2 точки касания с окружностью
4) прямая имеет 1 точку касания с окружностью
в мимо окружности в перпендикулярной плоскости
6) мимо окружности под углом к плоскости окружности
7) пролегает через центр окружности в перпендикулярной плоскости
8) пролегает через центр окружности под углом к плоскости окружности
9) прямая имеет 1 точку касания с окружностью в перпендикулярной плоскости
10) прямая имеет 1 точку касания с окружностью под углом к плоскости окружности
11) прямая имеет 1 точку касания с кругом в перпендикулярной плоскости
12) прямая имеет 1 точку касания с кругом под углом к плоскости окружности
48 : 4 = 12 (48 : 4 = 12)
92 : 4 = 23 (92 : 4 = 23)
184 : 4 = 46 (84 : 4 = 21)
996 : 4 = 249 (96 : 4 = 24)
1236 : 4 = 309 (36 : 4 = 9)
5556 : 4 = 1389 (56 : 4 = 14)
Доказательство:Если число является двузначным (или однозначным), то утверждение очевидно.
Если число является трехзначным (или "более -значным"), то оно представимо в виде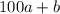 
(где 
- соответствующее натуральное число, а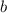 
- однозначное / двузначное число, образующееся двумя последними цифрами исходного числа).
Заметим, что: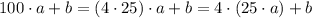 
. Так что 
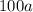всегда делится на 
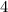. И если 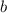тоже делится на 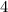, то искомое число, как сумма двух чисел, делящихся на 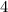( 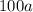и 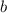), тоже будет делиться на .
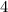Утверждение доказано!
