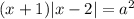
Первый аналитический)
1) Если 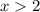 , то
, то 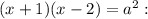
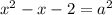
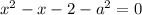
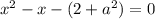
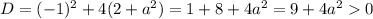
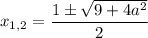
Проверим условие 
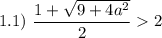
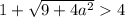
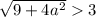
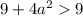
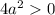
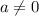
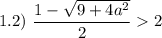
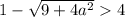
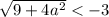
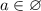
Таким образом, если 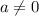 , то имеем корень
, то имеем корень 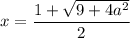
2) Если 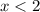 , то
, то 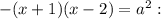
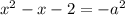
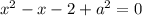
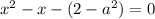
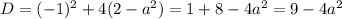
Найдем такие значения  , при которых
, при которых 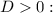
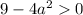
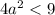
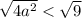
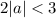
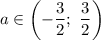
Тогда корни:
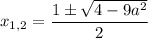
Проверим условие 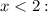
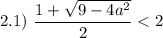

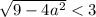
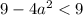
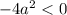
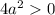
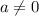
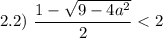

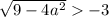
![a \in \left[-\dfrac{3}{2}; \ \dfrac{3}{2} \right]](/tpl/images/1359/4428/7966b.png)
С учетом 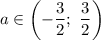 имеем:
имеем: 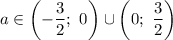
Таким образом, при 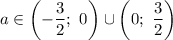 имеем три корня.
имеем три корня.
Второй графический)
Рассмотрим две функции:
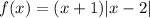
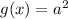 — линейная функция, график — прямая, параллельная оси абсцисс
— линейная функция, график — прямая, параллельная оси абсцисс
Изобразим на координатной плоскости функцию 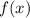
1) Если 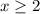 , то
, то 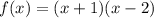 — квадратичная функция, график — парабола, ветви параболы направлены вверх
— квадратичная функция, график — парабола, ветви параболы направлены вверх
2) Если 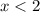 , то
, то 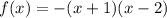 — квадратичная функция, график — парабола, ветви параболы направлены вниз
— квадратичная функция, график — парабола, ветви параболы направлены вниз
Вершина параболы: 
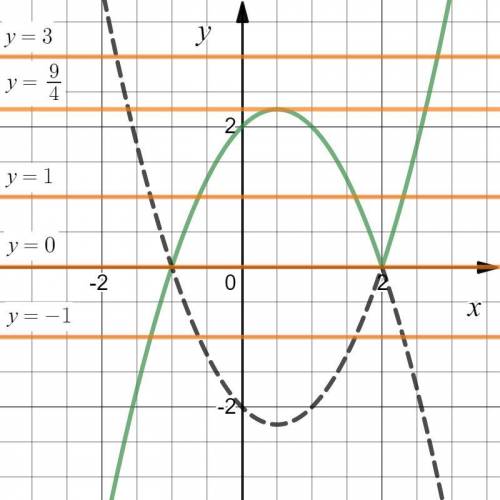
Изобразим данные функции на соответствующих участках (см. вложение).
Уравнение 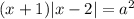 будет иметь три корня, если будет три пересечения графика функции
будет иметь три корня, если будет три пересечения графика функции 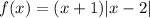 c
c 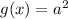
Так будет, если 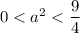 или
или 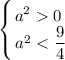
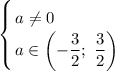
Решением системы будет 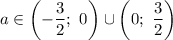
Таким образом, при 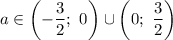 имеем три корня.
имеем три корня.
ответ: 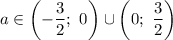
30 + 34 = 64*1/8 = 8
100 -86 = 14 *1/2 = 7
6 * 5 = 30 *1/5 = 6
64 : 8 = 8 *1/4 = 2