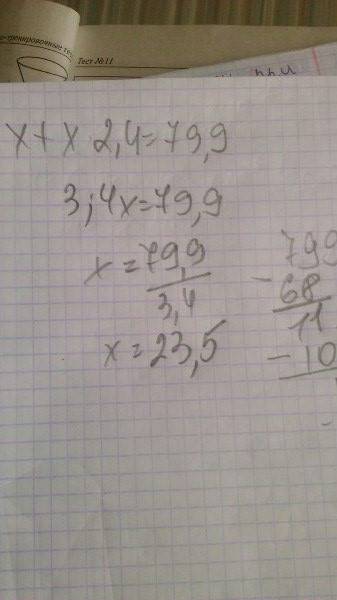
Пошаговое объяснение:
2/3 и 7/9
надо найти НОК у знаменателей:
3 = 3 * 1
9 = 3 * 3 * 1
НОК (3 и 9) = 3 * 3 * 1 = 9
9 : 3 = 3 тогда умножим 2/3 на 3 и числитель и знаменатель:
2 * 3 / 3 * 3 = 6/9
9 : 9 = 1 тогда 7/9 остается прежнем
получаем : 6/9 и 7/9
7/15 и 13/30
15 = 3 * 5 * 1
30 = 3 * 2 * 5 * 1
НОК (15 и 30) = 3 * 2 * 5 * 1 = 30
30 : 15 = 2 тогда 7 * 2/ 15 * 2 = 14/30
30 : 30 = 1 тогда 13/30 остается
получаем: 14/30 и 13/30
2/11 и 5/33
11 = 11 * 1
33 = 3 * 11 * 1
НОК (11 и 33) = 11 * 3 * 1 = 33
33 : 11 = 3 тогда 2 * 3 / 11 * 3 = 6/33
33 : 33 = 1 тогда 5/33 остается
получаем: 6/33 и 5/33
ответ: за 18 часов первый и за 36 часов второй ИЛИ за 60 часов первый и за 15 часов второй.
Пошаговое объяснение: Пусть работа по выкапыванию котлована 1 (единица), х часов время за которое первый экскаватор выполнит всю работу. Совместная производительность 1/12 (раб/час), производительность первого экскаватора 1/х (раб/час), производительность второго (1/12)-(1/х)=(х-12)/2х (раб/час). Если первый выполнит 1/3 работы, то времени затратит (1/3)÷(1/х)=(х/3) часа, второй выполнит остальную часть работы 1-(1/3)=(2/3), то времени он затратит (2/3)÷((х-12)/12х)=24х/(3х-36) часа, всего времени затратят 30 часов. Составим уравнение:
(х/3)+(24х/(3х-36))=30
3х²-36х+72х=270х-3240
3х²-234х+3240=0
х²-78х+1080=0
D=1764
х₁=18 (ч). За 18 часов, первый экскаватор выкопает котлован самостоятельно.
(1/12)-(1/18)=1/36 (раб/час) производительность второго экскаватора.
1÷(1/36)=36 (ч). За 36 часов, второй экскаватор выкопает котлован самостоятельно.
ИЛИ:
х₂=60 (ч) За 60 часов, первый экскаватор выкопает котлован самостоятельно.
(1/12)-(1/60)=1/15 (раб/час) производительность второго экскаватора.
1÷(1/15)=15 (ч). За 15 часов, второй экскаватор выкопает котлован самостоятельно.
3,4x=79,9
x=23,5