а) Обозначим точки пересечения лучей с отрезком BM — буквами P и R (см. рисунок), и пусть O — точка пересечения диагоналей параллелограмма, а N — точка пересечения луча AP и прямой BC.
Точка R делит медиану BM треугольника ABD в отношении 2 :1 считая от B. Следовательно, R лежит на медиане AO этого треугольника, то есть луч AR содержит диагональ AC .
б) Пусть L — точка пересечения AN и BD. Нужно найти площадь четырёхугольника LNCO. Пусть площадь параллелограмма равна S . Площадь треугольника BOC равна Найдём площадь треугольника BNL . Из подобия треугольников BPN и MPA следует, что
откуда
Теперь из подобия треугольников BNL и DAL следует, что их соответствующие высоты относятся как 1:4 , а поэтому высота треугольника BNL, проведённая к BN, составляет высоты параллелограмма, проведённой к стороне BC.
Поэтому
Следовательно, площадь четырёхугольника LNCO равна
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
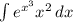Пусть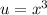 
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/5039/8c879.png)
.
![du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}](/tpl/images/1117/5039/82eee.png)
Делаем подстановку в наше изначальное выражение:
![\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }](/tpl/images/1117/5039/640b8.png)
Здесь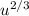 
сокращаются и мы имеем 
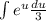. Выносим 
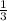за интеграл: 
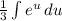. Теперь мы имеем знакомый интеграл, который равняется 
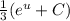, тоже самое что 
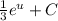. Подставляем 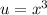и имеем 
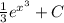. Используем фундаментальную теорему исчисления:
![\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}](/tpl/images/1117/5039/3089c.png)
