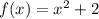 определена на множестве E
определена на множестве E 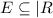
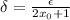 где
где 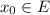 .
. на области
на области 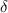 от
от  (то есть:
(то есть: 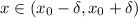 ) выполняется
) выполняется 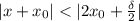 .
.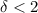 , выполняется
, выполняется 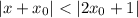 .
.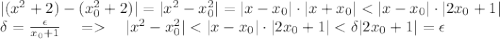
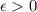 есть
есть 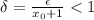 , на области которой выполняется
, на области которой выполняется 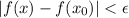
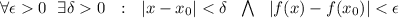 ). Следовательно -
). Следовательно - 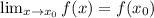 .
.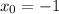 нужно отдельно доказать предел
нужно отдельно доказать предел 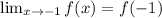 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 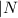 тоже подмножество
тоже подмножество  , значит
, значит 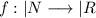 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 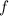 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 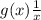 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 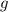 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 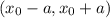 "...
"...849.
Пошаговое объяснение:
Справка:
Порядок действий в выражениях с несколькими действиями:
1. Выполняем действия I ступени (умножение и деление) в скобках.
2. Выполняем действия II ступени (сложение и вычитание) в скобках.
3. Выполняем действия I ступени (умножение и деление) за скобками.
4. Выполняем действия II ступени (сложение и вычитание) за скобками.
875 - 24 * 8 : 6 + ( 164 - 116 ) : 8
1) 164 - 116 = 48
2) 24 * 8 = 192
3) 192 : 6 = 32
4) 48 : 8 = 6
5) 875 - 32 = 843
6) 843 + 6 = 849
УДАЧИ! ОБРАЩАЙТЕСЬ!
(7+х)*2=18
14+2х=18
2х=18-14
2х=4
х=2 км/ч - скорость течения реки