Пошаговое объяснение:
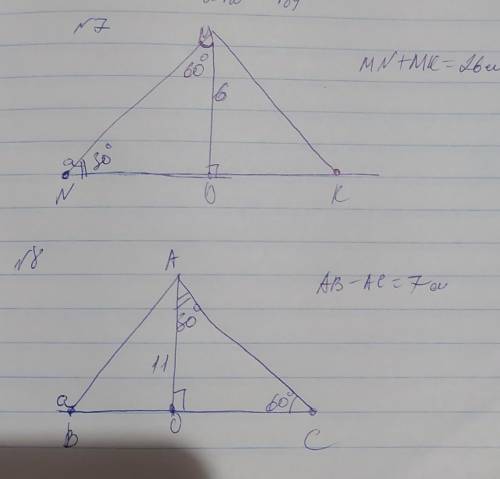
ЗАДАНИЕ 7
Перпендикуляр МО образует с прямой и наклонными 2 прямоугольных треугольника NMO и KMO, в которых наклонные являются гипотенуза и, а перпендикуляр и прямая - катеты. Рассмотрим ∆NMO. <NMO =60°- по условиям и так как сумма острых углов прямоугольного треугольника составляет 90°, тогда <N=90–60=30°
Катет МО, лежащий напротив угла 30° равен половине гипотенузы NM, поэтому MN=MO×2=6×2=12см.
Поскольку MN+MK=26см, то МК=26–MN=26–12=14см
ответ: MN=12см, МК=14см
ЗАДАНИЕ 8
Аналогично условиям в задаче 7: ∆ВАО и ∆САО - прямоугольные. Рассмотрим ∆САО, и если <С=60°, тогда найдём гипотенузу АС через синус угла С:
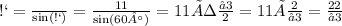
Поскольку АВ–АС=7, тогда АВ=7+АС=
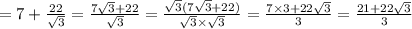
Можно так и оставить, но если нужно вычислить, то √3≈1,73, тогда:
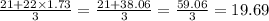
ответ: АВ≈19,69, АС=22/√3
Произведение двух натуральных чисел на 15 больше их наибольшего общего делителя, если это числа 16 и 1 или 6 и 3.
Пошаговое объяснение:
Обозначим числа a и b, их наибольший общий делитель обозначим d. Тогда ab-d=15
a можно представить как dx
b можно представить как dy. Тогда dx*dy-d=15 ⇔ d(dxy-1)=15
15 можно разложить на такие множители 1 и 15, а также 3 и 5. Соответственно, d=1 и dxy-1=15 или d=3 и dxy-1=5.
Рассмотрим первый случай: d=1 и dxy-1=15
Так как d=1, то xy-1=15 ⇔ xy=16 . Поскольку d - это наибольший общий делитель, то xy может быть произведением только 1 и 16. Тогда число a=1*1=1 и число b=1*16=16
Проверяем: ab=1*16=16
ab-d=16-1=15
Рассмотрим второй случай: d=3 и dxy-1=5
Так как d=3, то 3xy-1=5 ⇔ 3xy=6 ⇔ xy=2. Соответственно xy может быть произведением только 1 и 2. Тогда число a=3*1=3 и число b=3*2=6.
Проверяем: ab=3*6=18
ab-d=18-3=15
6 ед умножить на 5= 3 дес 6*5=30
18 ед разделить на 2= 9 ед 18:2=9
9 дес разделить на 3= 3 дес 90:3=30