Question

Впосёлке построили n дачных участков. n дачников, осмотрев участки, составили (каждый для себя) рейтинг участков: какой нравится больше всего, какой на втором месте, какой - на третьем, и так далее (ни одному из дачников никакие два участка не нравятся в равной степени). после случайного распределения участков между дачниками оказалось, что при любом другом распределении хотя бы один дачник получил менее нравящийся ему участок. докажите, что хотя бы один дачник получил участок, который ему нравится больше всего.

Answer 1

Докажем, что если после случайного распределения участков ни одному из дачников не достался лучший на его взгляд участок (*), то возможно перераспределить участки так, чтобы каждому достался более хороший на его взгляд участок. В условии же сказано, что распределение оказалось таково, что при любом другом, хотя бы одному достался бы более плохой участок. Если мы докажем вышеизложенное утверждение, то по противоречию будет следовать, что распределение не отвечает условию (*), а значит задача решена.

Рассмотрим таблицу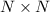 $N\times N$, где за строками скрываются дачники, а за столбцами - участки. В пересечении строки и столбца будет стоять число 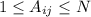$1\leq A_{ij}\leq N$, которое равно месту, которое отдал i-ый дачник j-ому участку.

Пусть произошло распределение по условию (*). Пусть i-ому участнику достался участок с местом (на его взгляд) i; Тогда существует $i-1$ участок, который лучше того, который ему достался. Аналогично для остальных дачников. Для того, чтобы перераспределить участки необходимо, чтобы сумма всех участков, которые лучше того, что достались дачнику была не меньше общего количества дачников (иначе были бы пересечения и на один участок претендовало бы не менее двух дачников). 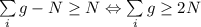То есть $\sum\limits_i g-N\geq N \Leftrightarrow \sum\limits_i g\geq 2N$; Так как никому не досталось первое место, а у каждого место не выше второго, то действительно сумма мест не меньше удвоенного количества дачников. Неравенство справедливо, а, значит, задача решена