Наименьшее значение функции f(3•π/4) = –1/2–√2/6
Наибольшее значение функции f(0) = 2/3
Пошаговое объяснение:
Стандартный алгоритм нахождения наименьшего и наибольшего значений функции f(x) на отрезке [a; b] следующее:
1) находим критические точки функции, которые входят в заданный отрезок [a; b], то есть найдем производную функции f(x) и находим нули производной на отрезке [a; b] (решаем уравнение f (x)=0);
2) вычислим значения функции f(x) для критических точек из отрезка [a; b] и для граничных значений a и b;
3) ответом будут наименьшее и наибольшее значения среди полученных значений функции.
1) находим критические точки функции f(x)=cosx–1/3•cos3x:
f'(x)=(cosx–1/3•cos3x)'= –sinx+sin3x
–sinx+sin3x=0
2•sinx•cos2x=0
a) sinx=0 или x=π•n, n∈Z
0 ≤ π•n ≤ π или n=0, 1, то есть x1=0 и x2=π;
b) cos2x=0 или 2x=π/2+π•k, k∈Z или x=π/4+π•k/2, k∈Z
0 ≤ π/4+π•k/2 ≤ π или –1/4 ≤ k/2 ≤ 3/4 или –1/2 ≤ k ≤ 3/2 или k=0, 1 или x3=π/4 и x4=3•π/4;
2) вычислим значения функции f(x) для критических точек x1=0, x2=π, x3=π/4 и x4=3•π/4 (граничные значения 0 и π находятся среди них):
f(0)= cos0–1/3•cos(3•0) = 1–1/3•1 = 2/3
f(π)= cosπ–1/3•cos(3•π) = –1–1/3•(–1) = –1+1/3 = –2/3
f(π/4) = cos(π/4)–1/3•cos(3•π/4) = √2/2–1/3•(–1/2) = 1/6+√2/2
f(3•π/4) = cos(3•π/4)–1/3•cos(9•π/4) = (–1/2)–1/3•cos(π/4) =
= –1/2–1/3•√2/2 = –1/2–√2/6
3) Для того чтобы найти наименьшее значение функции, нужно сравнить числа f(π)=–2/3 и f(3•π/4) =–1/2–√2/6:
f(π)–f(3•π/4) = –2/3–(–1/2–√2/6) = –2/3+1/2+√2/6 =
= (–4+3+√2)/6 = (√2–1)/6 > (√1–1)/6 = 0/6 = 0,
то есть f(π)>f(3•π/4) и наименьшее значение функции
f(3•π/4) = –1/2–√2/6.
Для того чтобы найти наибольшее значение функции, нужно сравнить числа f(0)=2/3 и f(π/4) =1/6+√2/2:
f(0)–f(π/4) = 2/3–(1/6+√2/2) = 2/3–1/6–√2/2 = (4–1–√2)/6 =
= (3–√2)/6 >(3–√4)/6 = (3–2)/6 = 1/6 > 0,
то есть f(0)>f(π/4) и наибольшее значение функции f(0) = 2/3.
100 человек
Пошаговое объяснение:
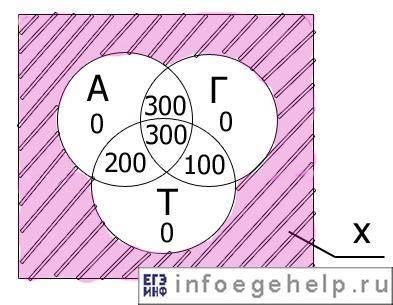
Число тех, кто не решил ни одной задачи возьмём за х
800 задач решили по алгебре
700 задач решили по геометрии
600 задач решили по тригонометрии
А+Г=600 школьников
А+Т=500 школьников
Г+Т=400 школьников
А+Г+Т= 300 школьников
1) А+Г+Т=800+700+600=2100 -всего решили задач по А,Г,Т
т.к. 300 человек (которые решили по три задачи) учтены при А+Г, А+Т, Г+Т определим сколько человек решили по две задачи.
2) А+Г=600 - 300=300 чел решили только две задачи А+Г
3) А+Т=500- 300 =200 чел решили только две задачи А+Т
4) Г+Т=400-300= 100 чел. решили только две задачи Г+Т
5) 300+200+100=600 человек решили две задачи
6) 600*2+300*3=1200+900=2100 задач решили школьники (которые решили по две и по три задачи)
7)2100-2100=0- задач решили школьники (которые решили только по одной задачи)
8) 300+600=900 школьников решили две и более задач
9) 1000-900=100 школьников ничего не решили
ответ: 100 школьников ничего не решили.
Ниже прикрепил картинку, чтобы было видно визуально
Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: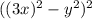
; В следующих двух слагаемых вынесем общий множитель "40": 
; В итоге получим следующее уравнение: 
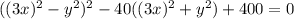. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 
будет стоять 
; Это приведет к тому, что придется убавить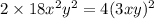 
; В итоге: 
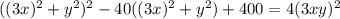; Слева стоит квадрат суммы. Уравнение примет вид: 
; Сворачивая еще раз: 
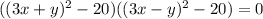; Получаем серию прямых: 
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом
; Рассмотрим прямую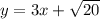 
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 
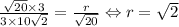; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 
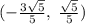; Ну а все решения: