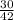 и
и 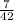
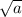 , то необходимо домножить и числитель, и знаменатель на этот корень (основное свойство дроби)
, то необходимо домножить и числитель, и знаменатель на этот корень (основное свойство дроби) или
или 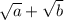 , то числитель и знаменатель необходимо домножить на сопряжённое выражение (для первого: на
, то числитель и знаменатель необходимо домножить на сопряжённое выражение (для первого: на 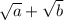 ; для второго выражения на
; для второго выражения на 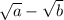 ), сведя числитель к формуле разности квадратов. Это алгоритм для квадратных корней. Для корней больше 2 степени сопряжённые ищутся иначе и по другим формулам.
), сведя числитель к формуле разности квадратов. Это алгоритм для квадратных корней. Для корней больше 2 степени сопряжённые ищутся иначе и по другим формулам.