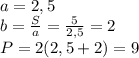
Упрощаем выражения 1) -4а • 5 = -4 • 5а = -20а, коэффициент - это число (-20); 2) 8b • (-3) = 8 • (-3) • b = -24b, коэффициент - это число (-24); 3) (-5c) • 2 = (-5) • 2 • с = -10с, коэффициент - это число (-10); 4) 4x • (-3) = 4 • (-3)• х = - 12х, коэффициент - это число (-12); 5) 9y • (-5) = 9• (-5)у = -45у, коэффициент - это число (-45); 6) (-7m) • (-8) = 56 m, коэффициент - это число 56; 7) m • (-3) • (-5) = 15m, коэффициент - это число 15; 8) n • 7 • (-2) = -14n, коэффициент - это число (-14); 9) (-k) • 5 • (-3) = 15k, коэффициент - это число 15.
Пошаговое объяснение:
Упрощаем выражения 1) -4а • 5 = -4 • 5а = -20а, коэффициент - это число (-20);
2) 8b • (-3) = 8 • (-3) • b = -24b,
коэффициент - это число (-24); 3) (-5c) • 2 = (-5) • 2 • с = -10с
коэффициент - это число (-10); 4) 4x • (-3) = 4 • (-3)• х = - 12х,
коэффициент - это число (-12); 5) 9y • (-5) = 9• (-5)у = -45у,
коэффициент - это число (-45); 6) (-7m) • (-8) = 56 m,
коэффициент - это число 56; 7) m • (-3) • (-5) = 15m,
коэффициент - это число 15; 8) n • 7 • (-2) = -14n,
коэффициент - это число (-14); 9) (-k) • 5 • (-3) = 15k, коэффициент - это число 15.
Куб натурального числа n можно представить в виде n слагаемых, образующих арифметическую прогрессию с разностью 2.
Доказательство:
Если n — число нечётное:
Пусть средний член равен n². Тогда сумма членов этой прогрессии равна n² + n² - 2 + n² + 2 + ... = n² + n² + n² + ... (n раз) = n² * n = n³.
Если n — число чётное:
Пусть средние члены (по счёту n/2 и n/2 + 1) равны n²-1 и n²+1. Сумма членов прогрессии равна: n² - 1 + n² + 1 + n² - 3 + n² + 3 + ... = n² + n² + n² + ... (n раз) = n² * n = n³.
Во всех возможных случаях мы смогли представить куб натурального числа в виде n слагаемых, что и требовалось доказать.
P=(12,5+2/5)*2=25,8 м