70
Пошаговое объяснение:
В первом ряду 20 книг .
Книги второго ряда в 1,2 раза > или больше чем в первом ряду.
Всегда знайте если в (число) раз(а) больше то мы умножаем а если меньше то делим. Запомните это правило.
1) 20*1,2=24 (кн.) во втором ряду книг.
Книги третьего ряда в 1,3 раза больше (я так думаю) чем во втором ряду.
2) 20*1,3=26 (кн.) в третьем ряду книг.
Мы решили сколько книг во втором и третьем рядах но у нас остался главный вопрос
Сколько книг в трёх рядах книжных полок?
Когда у нас вопрос сколько всего мы всегда все числа которые мы узнали должны прибавить и всё.
3) 20+24+26=70 (кн.) Всего
Надеюсь правильно решил и объяснил
777 литра
Пошаговое объяснение:
Пусть в 1-сосуде Х литр воды, а во 2-сосуде 0 литр воды.
1-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 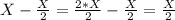
2-сосуд: 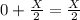
Объем воды в обоих сосудах в сумме дают Х литр!
2-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 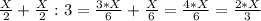
2-сосуд: 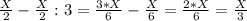
Объем воды в обоих сосудах в сумме дают Х литр!
3-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 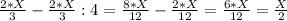
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
Теперь покажем, что в нечётных числах переливания всегда
1-сосуд: 
2-сосуд: 
Пусть n=2·k+1.
n-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 
2-сосуд: 
(n+1)-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 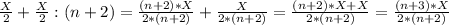
2-сосуд: 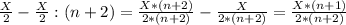
(n+2)-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 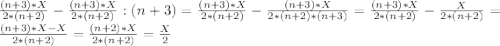
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
что требовалось показать.
Отсюда, 2019 - нечётное и X=1554 литра, тогда
1-сосуд: 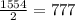
2. для q(x) также берем производную от F(x)=5x^4+4x^3-3x^2 F'(x)=20x^3+12x^2-6x=2x(10x^2+6x-3)
3. a) f(x)=6x^2+10x^4-3 берем интеграл неопределенный (S - интеграл)
F(x)= S (6x^2+10x^4-3)dx=6 x^3/3 +10 x^5 /5 -3x +const=2x^3+2x^5-3x+const
б) f(x)=9-8x+x^5 F(x) =S (9-8x+x^5)dx =9x - 4x^2+x^6 /6 +const
в) f(x)=x^2+x-1 F(x) =S( x^2+x-1)dx =x^3 /3 +x^2 /2 -x +const
4. найдем все первообразные функции f(x) => S(3x^2-2x+1)dx =x^3 -x^2+x +const
теперь найдем константу const => в полученное уравнение F(x)= x^3 -x^2+x +const подставим x= -1 y= 2 => 2=-1 -1 -1 +const => const =5
Искомая первообразная F(x) =x^3 -x^2+x +5