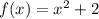 определена на множестве E
определена на множестве E 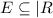
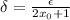 где
где 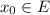 .
. на области
на области 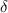 от
от  (то есть:
(то есть: 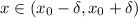 ) выполняется
) выполняется 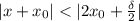 .
.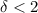 , выполняется
, выполняется 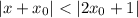 .
.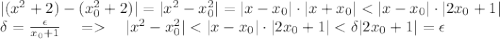
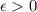 есть
есть 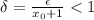 , на области которой выполняется
, на области которой выполняется 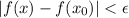
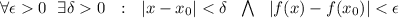 ). Следовательно -
). Следовательно - 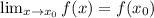 .
.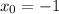 нужно отдельно доказать предел
нужно отдельно доказать предел 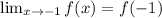 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 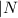 тоже подмножество
тоже подмножество  , значит
, значит 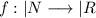 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 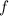 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 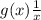 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 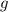 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 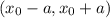 "...
"...
1) 3 = (1+1) + (1/3 + 2/3) = 1ц1/3 + 1ц2/3;
2) 5 = (1+3) + (2/7 + 5/7) = 1ц2/7 + 3ц5/7;
3) 8 = (3+4) + (2/5 + 3/5) = 3ц2/5 + 4ц3/5;
4) 9 = (3+5) + (1/4 + 3/4) = 3ц1/4 + 5ц3/4.
Поскольку в условии никаких требований, кроме равенства знаменателей, к смешанным числам нет, данные в задании числа можно разбивать произвольно, но так,чтобы числитель в одном из чисел не сокращался со знаменателем, меняя его.