1.41
Пошаговое объяснение:
Ну, пусть искомое число - это х,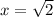 
. Тогда
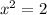
Но мы знаем, что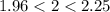 
- это очевидно. Тогда извлечём корень, и в силу его монотонного возрастания, знаки не поменяются. Тогда
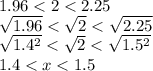
Отлично, мы определили х до первого знака после запятой. Определим его и до второй.
Есть такое число, 1.9881 = 1.41² и 2.0164 = 1.42²
Очевидно, что вот так:
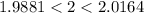
Тогда опять же из-за прекрасной функции корня получаем красивую вещь:
То есть, так как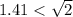 
, то 
, наибольший порядок у у равен порядку 1.41 - а это -2. Тогда у не будет влиять на второй знак после запятой в числе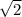 
, тогда 1.41 - десятичная запись 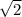до второго знака.
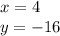
Пошаговое объяснение:
Т.к. функция косинус в левой части первого уравнения системы и квадратичная функция в правой части являются "функциями из разных разделов математики", то попытаемся оценить их:
Известно, что модуль косинуса не превосходит 1, а значит:
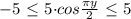
По виду квадратичной функции можно определить, что это парабола с ветвями вверх, а значит верхнего предела у нее нет.
Нижний предел равен значению функции в вершине параболы, который можно найти или взятием производной, или с готовой формулы. Для этого найдем абсциссу вершины параболы, а затем подставим найденное значение в функцию:
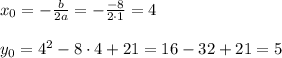
Это значит, что:
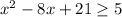
При сравнении полученных неравенств становится ясно, что эти функции равны только тогда, когда обе функции равны 5.
Решим отдельно тригонометрическое уравнение
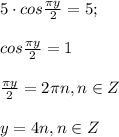
ответ получился не единственный, поэтому воспользуемся вторым уравнением системы и подставим в него найденные значения для x и y:
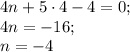
Отсюда можем найти конкретное значение для y:
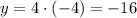
Окончательный ответ:
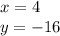
1) 4(m-3n) - (k+c) = 4m - 4*3n-k-c = 4m-12n-k-c.
2)1.3(2a-5) - 4(b+3) = 1.3*2a - 5*1.3 -4b-4*3 = 2.6a-6.5-4b-12 = 2.6a-4b-18.5.
3)0.2(3m+8)+(-n-2) = 0.2*3m+0.2*8-n-2 = 0.6m+1.6-n-2 = 0.6m-n-0.4.